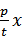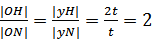- 简单曲线的极坐标方程
- 共19题
20.
在直角坐标系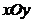
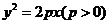
(I)求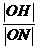
(II)除H以外,直线MH与C是否有其它公共点?说明理由.
正确答案
解:将直线l与抛物线联立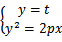

(1) ∵ M关于P的对称点为N ∴ 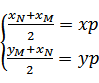


∴ ON直线斜率 kON=
则H点坐标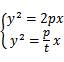

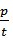

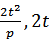
∴
(2)由①知kMH=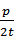
与抛物线联立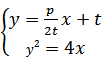
即y2-4ty+4t2=0 ∴ △=16t2-4x4t2=0 ∴ 直线MH与抛物相切
∴ 直线MH与曲线C除点H外没有其它公共点
知识点
选做题:请考生在第22、23、24三题中任选一题做答,如果多做,则按所做的第一题记分.
22.选修4—1:几何证明选讲
如图,










(1)求证:



(2)求证:
23.选修4-4:坐标系与参数方程
已知平面直角坐标系




(1)写出曲线C的普通方程和极坐标方程;
(2)求|AB|的值。
24.选修4-5:不等式选讲
已知


(1)当

(2)如果函数

正确答案
22.
证明:
(1)连接

又
又
所以
所以



(2)延长


因为
所以

23.
解:
(1)曲线C的参数方程为:
消参数
由曲线C的普通方程为:
所以曲线C的极坐标方程为:
(2)由点A,B的极坐标分别为:
得点A,B的直角坐标分别为:
所以
24.
解:
(1){x|x≥2或x≤-4}.
(2)(-2,2)
①当a=1时,f(x)=|2x-1|+x-5=
由

∴f(x)≥0的解为{x|x≥2或x≤-4}.
②由f(x)=0得|2x-1|=-ax+5.作出y=|2x-1|和y=-ax+5 的图象
观察可以知道,当-2<a<2时,这两个函数的图象有两个不同的交点,函数y=f(x)有两个不同的零点.故a的取值范围是(-2,2).
解析
解析已在路上飞奔,马上就到!
知识点
在极坐标系中, 圆p=4 sin

正确答案
解析
把圆p=4 sin





知识点
已知曲线





(1)把
(2)求


正确答案
见解析
解析
解析:将


即




(2)

由


所以



知识点
选做题(14、15题,考生只能从中选作一题)
14.在平面直角坐标系









15.如图













正确答案
14.
15.3
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析