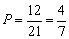- 随机事件的频率与概率
- 共77题
甲、乙两位学生参加数学竞赛培训,现分别从他们在培训期间参加的若干次预赛成绩中随机抽取8次,记录如下:
(1)画出甲、乙两位学生成绩的茎叶图,指出学生乙成绩的中位数;
(2)现要从中选派一人参加数学竞赛,从平均状况和方差的角度考虑,你认为派哪位学生参加合适?请说明理由;
(3)若将频率视为概率,对学生甲在今后的三次数学竞赛成绩进行预测,记这三次成绩中高于80分的次数为


正确答案
见解析。
解析
(1)茎叶图如下:
学生乙成绩中位数为84。
(2)派甲参加比较合适,理由如下:



(3)记“甲同学在一次数学竞赛中成绩高于80分”为事件A,则
随机变量
且





知识点
沙糖桔是柑桔类的名优品种,因其味甜如砂糖故名,某果农选取一片山地种植沙糖桔,收获时,该果农随机选取果树20株作为样本测量它们每一株的果实产量(单位:kg),获得的所有数据按照区间



(1)求a, b的值;
(2)从样本中产量在区间

正确答案
见解析。
解析
知识点
某工厂有三个车间,共有员工2000名,各车间男、女员工人数如下表:
已知在全厂员工中随机抽取1名,抽到第二车间女员工的概率是0.19。
(1)求x,y的值;
(2)现用分层抽样的方法在第三车间抽取5名员工参加志愿者活动,将这5人看做一个总体,现要从5人中任选2人做正、副组长,求恰好有一名女员工当选正组长或副组长的概率。
正确答案
见解析。
解析
知识点
某学校有两个参加国际中学生交流活动的代表名额,为此该校高中部推荐了2男1女三名候选人,初中部也推荐了1男2女三名候选人。
(1)若从初高中各选1名同学做代表,求选出的2名同学性别相同的概率;
(2)若从6名同学中任选2人做代表,求选出的2名同学都来自高中部或都来自初中部的概率。
正确答案
(1)
(2)
解析
设高中部三名候选人为A1,A2,B,初中部三名候选人为a,b1,b2
(1)由题意,从初高中各选1名同学的基本事件有
(A1,a),(A1,b1),(A1,b2),
(A2,a),(A2,b1),(A2,b2),
(B,a),(B,b1),(B,b2), 共9种 ……2分
设“2名同学性别相同”为事件E,则事件E包含4个基本事件,
概率P(E)=
所以,选出的2名同学性别相同的概率是
(2)由题意,从6名同学中任选2人的基本事件有
(A1 ,A2),(A1,B),(A1,a),(A1,b1),(A1,b2),
(A2,B), (A2,a),(A2,b1),(A2,b2),(B,a),
(B,b1),(B,b2),(a,b1),(a,b2),(b1,b2) 共15种 ……8分
设“2名同学来自同一学部”为事件F,则事件F包含6个基本事件,
概率P(F)=
所以,选出的2名同学都来自高中部或都来自初中部的概率是
知识点
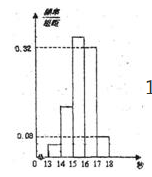
为了了解某年段1000名学生的百米成绩情况,随机抽取了若干学生的百米成绩,成绩全部介于13秒与18秒之间,将成绩按如下方式分成五组:第一组[13,14);第二组[14,15);……;第五组[17,18],按上述分组方法得到的频率分布直方图如图所示,已知图中从左到右的前3个组的频率之比为3:8:19,且第二组的频数为8.
(1)将频率当作概率,请估计该年段学生中百米成绩在[16,17)内的人数;
(2)求调查中随机抽取了多少个学生的百米成绩;
(3)若从第一、五组中随机取出两个成绩,求这两个成绩的差的绝对值
大于1秒的概率,
正确答案
见解析。
解析
(1)百米成绩在[16,17)内的频率为0.32×1=0.32. 0.32×1000=320
∴估计该年段学生中百米成绩在[16,17)内的人数为320人
(2)设图中从左到右前3个组的频率分别为3x,8x,19x依题意:得3x+8x+19x+0.32×1+0.08×1=1,
∴x=0.02
设调查中随机抽取了n个学生的百米成绩,则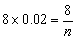
∴调查中随机抽取了50个学生的百米成绩.
(3)百米成绩在第一组的学生数有3×0.02×1×50=3,记他们的成绩为,a,b,c
百米成绩在第五组的学生数有0.08×1×50=4,记他们的成绩为m,n,p,q
则从第一、五组中随机取出两个成绩包含的基本事件有
{a,b},{a,c},{a,m},{a,n},{a,p},{a,q},{b,c},{b,m},{b,n},
{b,p},{b,q},{c,m},{c,n},{c,p},{c,q},{m,n},{m,p},{m,q},{n,p},{n,q},
{p,q}, 共21个
其中满足成绩的差的绝对值大于1秒所包含的基本事件有{a,b},{a,n},{a,p},{a,q},
{n,m},{b,n},{b,p},{b,q},{c,m},{c,n},{c,p},{c,q},共12个,
所以
知识点
扫码查看完整答案与解析