- 随机事件的频率与概率
- 共77题
8.已知下列三个命题:
①若两组数据的平均数相等,则它们的标准差也相等
②在区间
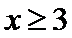
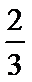
③直线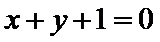
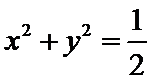
其中真命题的个数是( )
正确答案
解析
1)根据平均数、方差与标准差的性质可知①错误
2)根据与长度有关的几何概型可知正确为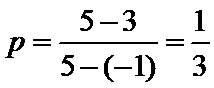
3)根据直线与圆的位置关系,圆心到直线的距离为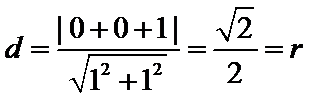
∴ 选B
考查方向
解题思路
直接法对每一个判断
1)根据平均数、方差与标准差的性质可知①错误
2)根据与长度有关的几何概型可知正确为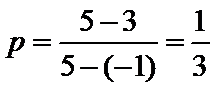
3)根据直线与圆的位置关系,圆心到直线的距离为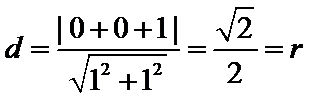
易错点
本题属于数学中的多选题,易错于对个别判断错误导致选择错误,
知识点
已知某中学高三文科班学生共有



(Ⅰ)如果从第




(Ⅱ)抽的
21.成绩分为优秀、良好、及格三个等级,横向、纵向分别表示地理成绩与数学成绩,例如:表中数学成绩为良好的共有


22.将



正确答案
(1)

解析
(Ⅰ)依题意,最先检测的3个人的编号依次为
(Ⅱ)由

因为

考查方向
解题思路
1)第一问考察统计的知识,比较简单,直接由比例可得出
2)第二问中属于古典概型,较简单,直接列举出所有的情况,数出个数作商。
易错点
容易在找出满足条件的所有事件时丢掉。
正确答案
(2)
解析
(Ⅲ)由题意,知

故满足条件的



其中数学成绩为优秀的人数比及格的人数少有:


∴数学成绩优秀的人数比及格的人数少的概率为
考查方向
解题思路
1)第一问考察统计的知识,比较简单,直接由比例可得出
2)第二问中属于古典概型,较简单,直接列举出所有的情况,数出个数作商。
易错点
容易在找出满足条件的所有事件时丢掉。
某市为庆祝北京夺得











16.若电视台记者要从抽取的群众中选


17.已知第




正确答案
(Ⅰ)
解析
(Ⅰ)设第



被采访人恰好在第


∴估计被采访人恰好在第

考查方向
解题思路
根据题中给出的频率分布直方图求出第(1)问的答案;
易错点
列基本事件的个数时多数或少数。
正确答案
(Ⅱ)
解析
(Ⅱ)第


∴第


记第




从第



至少有一名女性群众包含
共
∴从第



考查方向
解题思路
求出各组中的群众人数,后数出所有的基本事件的个数和事件 至少有一名女性群众所包含的基本事件的个数相除即可。
易错点
列基本事件的个数时多数或少数。
17. 有两个袋子,其中甲袋中装有编号分别为1、2、3、4的4个完全相同的球,乙袋中装有编号分别为2、4、6的3个完全相同的球.
(I)从甲、乙袋子中各取一个球,求两球编号之和小于8的概率;
(II)从甲袋中取2个球,从乙袋中取一个球,求所取出的3个
正确答案
见解析
解析
所以含有编号为2的球的概率
考查方向
解题思路
写出基本事件空间,并用古典概型的概率公式计算概率
易错点
本题易错在第一问分类不清
知识点
6. 在区间



正确答案
解析
命题“





考查方向
解题思路
由命题为真命题,可得
易错点
容易将区域画错
知识点
扫码查看完整答案与解析












