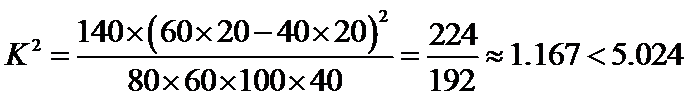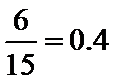随机事件的频率与概率_章节学习

1

题型：简答题

|

简答题 · 12 分

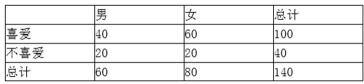
周立波是海派清口创始人和《壹周·立波秀》节目的主持人，他的点评视角独特，语言幽默犀利，给观众留下了深刻的印象．某机构为了了解观众对《壹周·立波秀》节目的喜爱程度，随机调查了观看了该节目的140名观众，得到如下的列联表：（单位：名）

19.从这60名男观众中按对《壹周·立波秀》节目是否喜爱采取分层抽样，抽取一个容量为6的样本，问样本中喜爱与不喜爱的观众各有多少名？

20，根据以上列联表，问能否在犯错误的概率不超过0.025的前提下认为观众性别与喜爱《壹周·立波秀》节目有关．（精确到0.001）

21.从19题中的6名男性观众中随机选取两名作跟踪调查，求选到的两名观众都喜爱《壹周·立波秀》节目的概率．

第(1)小题正确答案及相关解析

正确答案

喜爱的观众有4名；不喜爱的观众有2名．

解析

抽样比为，则样本中喜爱的观众有40×=4名；不喜爱的观众有6﹣4=2名．

考查方向

分层抽样的统计方法

解题思路

直接计算抽样比，即可算出喜爱与不喜爱的人数；

易错点

对“独立性检验的思想”不理解易出错

第(2)小题正确答案及相关解析

正确答案

不能在犯错误的概率不超过0．025的前提下认为观众性别与喜爱有关．

解析

假设：观众性别与喜爱无关，由已知数据可求得，

∴ 不能在犯错误的概率不超过0．025的前提下认为观众性别与喜爱有关．

考查方向

独立性检验的思想及其初步应用.

解题思路

直接代入公式计算,通过表中数据得出相应结论

易错点

对“独立性检验的思想”不理解易出错

第(3)小题正确答案及相关解析

正确答案

0.4

解析

记喜爱的4名男性观众为a，b，c，d，不喜爱的2名男性观众为1，2；则基本事件分别为：（a，b），（a，c），（a，d），（a，1），（a，2），（b，c），（b，d），（b，1），（b，2），（c，d），（c，1），（c，2），（d，1），（d，2），（1，2）．

其中选到的两名观众都喜爱的事件有6个，

故其概率为P（A）=

考查方向

等可能事件的概率

解题思路

直接列出总事件及发生事件的情况，直接求比。

易错点

对“独立性检验的思想”不理解易出错

1

题型：单选题

|

单选题 · 5 分

4．口袋中有四个小球，其中一个黑球三个白球，从中随机取出两个球，则取到的两个球同色的概率为

A

B

C

D

正确答案

B

解析

先记“黑球”为“” “白球”为“”，用列举法列出所有的基本事件：，数出个数；

符合两球同色的基本事件：，并数出个数；

。

考查方向

本题主要考查了古典概率模型概率的计算。

解题思路

利用古典概率模型的解题步骤解题；用列举法列出所有的基本事件，再找到符合两球同色的基本事件个数，利用古典概率模型的概率公式求解。

易错点

基本事件总数出错。

知识点

随机事件的频率与概率

1

题型：简答题

|

单选题

治疗慢性支气管炎肝火犯肺证，应首选

A．四逆散合左金丸
B．泻白散合黛蛤散
C．柴胡疏肝散
D．清金化痰汤
E．桑白皮汤

正确答案

B

解析

暂无解析

1

题型：简答题

|

简答题 · 12 分

周立波是海派清口创始人和《壹周·立波秀》节目的主持人，他的点评视角独特，语言幽默犀利，给观众留下了深刻的印象．某机构为了了解观众对《壹周·立波秀》节目的喜爱程度，随机调查了观看了该节目的140名观众，得到如下的列联表：（单位：名）

19.从这60名男观众中按对《壹周·立波秀》节目是否喜爱采取分层抽样，抽取一个容量为6的样本，问样本中喜爱与不喜爱的观众各有多少名？

20，根据以上列联表，问能否在犯错误的概率不超过0.025的前提下认为观众性别与喜爱《壹周·立波秀》节目有关．（精确到0.001）

21.从19题中的6名男性观众中随机选取两名作跟踪调查，求选到的两名观众都喜爱《壹周·立波秀》节目的概率．

第(1)小题正确答案及相关解析

正确答案

喜爱的观众有4名；不喜爱的观众有2名．

解析

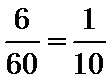
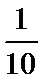
抽样比为，则样本中喜爱的观众有40×=4名；不喜爱的观众有6﹣4=2名．

考查方向

分层抽样的统计方法

解题思路

直接计算抽样比，即可算出喜爱与不喜爱的人数；

易错点

对“独立性检验的思想”不理解易出错

第(2)小题正确答案及相关解析

正确答案

不能在犯错误的概率不超过0．025的前提下认为观众性别与喜爱有关．

解析

假设：观众性别与喜爱无关，由已知数据可求得，

∴ 不能在犯错误的概率不超过0．025的前提下认为观众性别与喜爱有关．

考查方向

独立性检验的思想及其初步应用.

解题思路

直接代入公式计算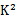,通过表中数据得出相应结论

易错点

对“独立性检验的思想”不理解易出错

第(3)小题正确答案及相关解析

正确答案

0.4

解析

记喜爱的4名男性观众为a，b，c，d，不喜爱的2名男性观众为1，2；则基本事件分别为：（a，b），（a，c），（a，d），（a，1），（a，2），（b，c），（b，d），（b，1），（b，2），（c，d），（c，1），（c，2），（d，1），（d，2），（1，2）．

其中选到的两名观众都喜爱的事件有6个，

故其概率为P（A）=

考查方向

等可能事件的概率

解题思路

直接列出总事件及发生事件的情况，直接求比。

易错点

对“独立性检验的思想”不理解易出错

1

题型：填空题

|

填空题 · 5 分

14.甲乙两人做游戏，游戏的规则是：两人轮流从1（1必须报）开始连续报数，每人一次最少要报一个数，最多可以连续报7个数（如，一个人先报数“1，2”，则下一个人可以有“3”， “3，4”，…，“3，4，5，6，7，8，9”等七种报数方法），谁抢先报到“100”则谁获胜.如果从甲开始，则甲要想必胜，第一次报的数应该是 .

正确答案

1，2，3，4

解析

甲先报1，2，3，4，然后不管乙报几个数，甲只需要每次报的数的个数与乙的个数

和为8（显然这可以做到），因为100－4＝96＝8×12 ，于是12轮过后，甲获胜．

故此题答案为1，2，3，4。

考查方向

本题主要属于数字问题，考查了数字的倍数等有关知识，意在考查考生分析问题解决问题的能力，逻辑推理能力，较难。

解题思路

本题总数为8的倍数时，对方先报，自己就一定能报到最后一个数，100=6×16+4=12×8+4。如果甲先报数，就先报4个数，100-4=96。然后无论乙报几个数，甲所报个数与乙的个数之各为8，这样保证甲一定获胜。

易错点

本题不易读懂题意，特别是对“每人一次最少要报一个数，最多可以连续报7个数”的理解不到位。本题易出现逻辑上的混乱，从而导致判断出错。

知识点

随机事件的频率与概率

1

题型：单选题

|

单选题 · 5 分

6. 在区间内随机取两个数，则使得“命题‘，不等式恒成立’为真命题”的概率为（）

A

B

C

D

正确答案

D

解析

命题“，不等式恒成立”为真命题,则有,所以概率为(4-) ，所以选D。

考查方向

本小题考查几何概型

解题思路

由命题为真命题，可得,如图，可算出概率.

易错点

容易将区域画错

知识点

四种命题及真假判断随机事件的频率与概率

1

题型：填空题

|

填空题 · 5 分

14．从字母a、b、c、d、e中任取两个不同的字母，则取到字母a的概率为_____.

正确答案

解析

所有取法列举为ab,ac,ad,ae,bc,bd,be,cd,ce,de共10种，其中取到a的方法有4种，故所求概率是4/10=2/5.

考查方向

本题考查古典概型。

解题思路

求出所有取法和符合条件的取法，作商即可。

易错点

计数出错。

教师点评

本题考查了古典概率知识，在近几年的各省高考题出现的频率较高，常与计数等知识点交汇命题。

知识点

随机事件的频率与概率

热门试卷

正确答案

解析

考查方向

解题思路

易错点

正确答案

解析

考查方向

解题思路

易错点

正确答案

解析

考查方向

解题思路

易错点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

正确答案

解析

考查方向

解题思路

易错点

正确答案

解析

考查方向

解题思路

易错点

正确答案

解析

考查方向

解题思路

易错点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

教师点评

知识点