- 随机事件的关系
- 共394题
由不等式





正确答案
解析
平面区域













知识点
甲乙两班进行消防安全知识竞赛,每班出3人组成甲乙两支代表队,首轮比赛每人一道必答题,答对则为本队得1分,答错不答都得0分,已知甲队3人每人答对的概率分别为


(1)求随机变量

(2)求在甲队和乙队得分之和为4的条件下,甲队比乙队得分高的概率。
正确答案
见解析。
解析
(1)




(2)设
则

知识点
盒内有大小相同的9个球,其中2个红色球,3个白色球,4个黑色球. 规定取出1个红色球得1分,取出1个白色球得0分,取出1个黑色球得-1分 . 现从盒内任取3个球
(1)求取出的3个球中至少有一个红球的概率;
(2)求取出的3个球得分之和恰为1分的概率;
(3)设
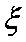
正确答案
见解析
解析
(1)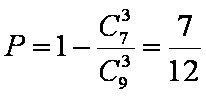
(2)记 “取出1个红色球,2个白色球”为事件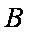
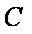
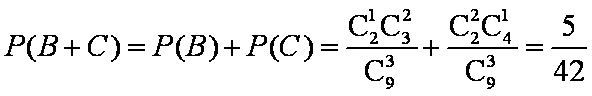
(3)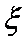
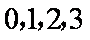
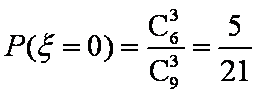
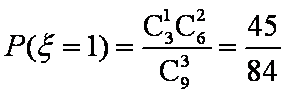
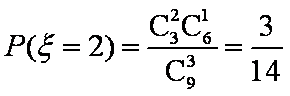
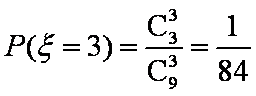
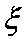
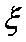
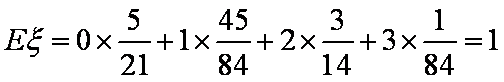
知识点
某机床厂今年年初用98万元购进一台数控机床,并立即投入生产使用,计划第一年维修、保养费用12万元,从第二年开始,每年所需维修、保养费用比上一年增加4万元,该机床使用后,每年的总收入为50万元,设使用x年后数控机床的盈利额为y万元。
(1)写出y与x之间的函数关系式;
(2)从第几年开始,该机床开始盈利(盈利额为正值)。
正确答案
(1)y=
解析
解析:(1)第二年所需维修、保养费用为12+4万元,
第

维修、保养费用成等差数列递增,依题得:


(2)由(1)可知当
解不等式
得
∵

知识点
今年来,随着地方经济的发展,劳务输出大省四川、河南、湖北、安徽等地的部分劳务人员选择了回乡就业,因而使得沿海地区出现了一定程度的用工荒.今年春节过后,沿海某公司对来自上述四省的务工人员进行了统计(见下表):
为了更进一步了解员工的来源情况,该公司

(1)从参加问卷调查的50名务工人员中随机抽取两名,求这两名来自同一个省份的概率;
(2)在参加问卷调查的50名务工人员中,从来自四川、湖北两省的人员中随机抽取两名,用ξ表示抽得四川省务工人员的人数,求ξ的分布列和数学期望。
正确答案
见解析
解析
(1)易得问卷调查中,从上述四省抽取的人数分别为
设“从参加问卷调查

从参加问卷调查的

这两名人




∴
(2)由(1)知,在参加问卷调查的







∴
知识点
扫码查看完整答案与解析




























