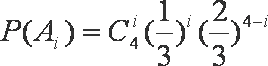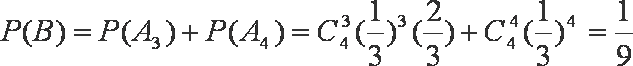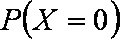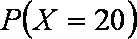- 随机事件的关系
- 共394题
现有4个人去参加某娱乐活动,该活动有甲、乙两个游戏可供参加者选择,为增加趣味性,约定:每个人通过掷一枚质地均匀的骰子决定自己去参加哪个游戏,掷出点数为1或2的人去参加甲游戏,掷出点数大于2的人去参加乙游戏。
(1)求这4个人中恰有2人去参加甲游戏的概率;
(2)求这4个人中去参加甲游戏的人数大于去参加乙游戏的人数的概率;
(3)用X,Y分别表示这4个人中去参加甲、乙游戏的人数,记ξ=|X-Y|,求随机变量ξ的分布列与数学期望Eξ.
正确答案
见解析
解析
解析:依题意,这4个人中,每个人去参加甲游戏的概率为,去参加乙游戏的概率为.设“这4个人中恰有i人去参加甲游戏”为事件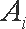
(1)这4个人中恰有2人去参加甲游戏的概率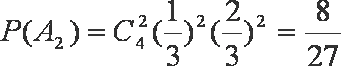
(2)设“这4个人中去参加甲游戏的人数大于去参加乙游戏的人数”为事件B,则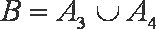
由于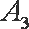

所以,这4个人去参加甲游戏的人数大于去参加乙游戏的人数的概率为. 7分
(3)ξ的所有可能取值为0,2,4. 由于



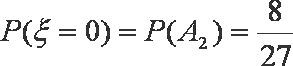
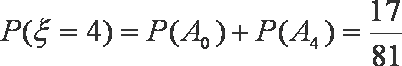
所以ξ的分布列是
随机变量ξ的数学期望
知识点
在游乐场,有一种游戏是向一个画满均匀方格的桌面上投硬币,若硬币恰落在任何一个方格内不与方格线重叠,即可获奖,已知硬币的直径为


正确答案
解析
设方格边长为

知识点
如图,长为m+1(m>0)的线段AB的两个端点A和B分别在

(1)求点M的轨迹Γ的方程,并判断轨迹Γ为何种圆锥曲线;
(2)设过点Q( ,0)且斜率不为0的直线交轨迹Γ于C,D两点.设点P在

正确答案
见解析
解析
(1)设A、B、M的坐标分别为(x0,0)、(0,y0)、(x,y),则x+y=(m+1)2, ①1分
由=m,得(x-x0,y)=m(-x,y0-y),
∴ ② ………………2分
将②代入①,得(m+1)2x2+()2y2=(m+1)2,
化简即得点M的轨迹Γ的方程为x2+=1(m>0),…………4分
当0<m<1时,轨迹Γ是焦点在x轴上的椭圆;
当m=1时,轨迹Γ是以原点为圆心,半径为1的圆;
当m>1时,轨迹Γ是焦点在y轴上的椭圆。 ……………6分
(2)依题意,设直线CD的方程为x=ty+,
消去x并化简整理,
△=m4t2+3m2(m2t2+1)>0,设C(x1,y1),D(x2,y2),则
y1+y2=-,y1y2=-。 ③ ……………………9分
设定点P(a,0),若
即直线PC、PD的倾斜角互补,
∴kPC+kPD=0, …………………………10分
即+=0,∵x1=ty1+,x2=ty2+,
化简,得4ty1y2+(1-2a)( y1+y2)=0, ④ ……………………11分
将③代入④,得+=0,即2m2t(2-a)=0,
∵m>0,∴t(2-a)=0,∵上式对∀t∈R都成立,∴a=2。
故定点P的坐标为(2,0)。 ……………………12分
知识点
为了解心肺疾病是否与年龄相关,现随机抽取了40名市民,得到数据如下表:
已知在全部的40人中随机抽取1人,抽到不患心肺疾病的概率为
(1)请将
(2)已知大于40岁患心肺疾病市民中,经检查其中有4名重症患者,专家建议重症患者住院治疗,现从这16名患者中选出两名,记需住院治疗的人数为

(3)能否在犯错误的概率不超过0.01的前提下认为患心肺疾病与年龄有关?
下面的临界值表供参考:
(参考公式:

正确答案
见解析
解析
解析:(1)
…………4分
(2)


(3)
所以在犯错误的概率不超过0.01的前提下认为患心肺疾病与年龄有关。 …………12分
知识点
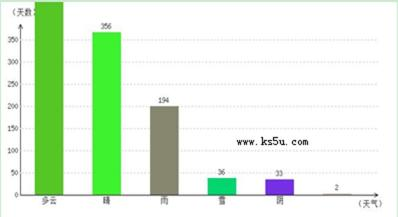
从天气网查询到邯郸历史天气统计 (2011-01-01到2014-03-01)资料如下:
自2011-01-01到2014-03-01,邯郸共出现:多云507天,晴356天,雨194天,雪36天,阴33天,其它2天,合计天数为:1128天。
本市朱先生在雨雪天的情况下,分别以

(1)求他某天打出租上班的概率;
(2)将他每天上班所需的费用记为

正确答案
见解析
解析
解析:(1)设


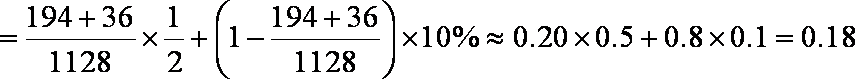
(2)
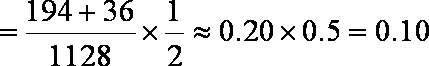
∴

知识点
扫码查看完整答案与解析