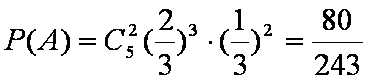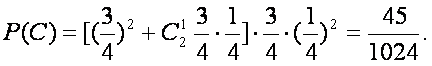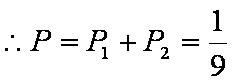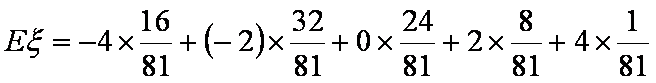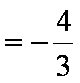- 随机事件的关系
- 共394题
已知椭圆







(1)求椭圆
(2)设













正确答案
见解析
解析
解:(1)由题意得:


(2)解:设


联立

解得
直线



又直线
因为


直线


令



又因为



化简得:
又C在直线

联立①、② 解得

又

解法二:因为
所以

设

联立


直线



由

知识点
甲、乙两人各射击一次,击中目标的概率分别是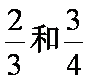
(1)求甲射击5次,有两次未击中目标的概率;
(2)假设某人连续2次未击中目标,则中止其射击,求乙恰好射击5次后,被中止射击的概率。
正确答案
见解析
解析
解:(1)设“甲射击5次,有两次未击中目标”
为事件A,则
(2)设“乙恰好射击5次后,被中止射击”为事件C,由于乙恰好射击5次后被中止射击,所以必然是最后两次未击中目标,第一次及第二次至多次有一次未
击中目标,则
知识点
学校游园活动有这样一个游戏项目:甲箱子里装有





(1)求在
①摸出
②获奖的概率;
(2)求在


正确答案
见解析
解析
解:(1)①解:设“在

②解:设“在1次游戏中获奖”为事件


且

(2)解:由题意可知



所以
所以

知识点
一个袋中有大小相同的标有1,2,3,4,5,6的6个小球,某人做如下游戏,每次从袋中拿一个球(拿后放回),记下标号。若拿出球的标号是3的倍数,则得1分,否则得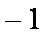
(1)求拿4次至少得2分的概率;
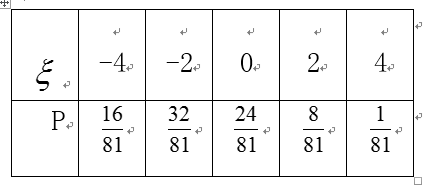
(2)求拿4次所得分数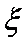
正确答案
见解析
解析
解(1)设拿出球的号码是3的倍数的为事件A,则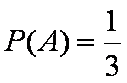
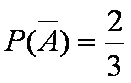
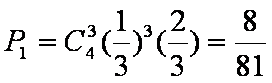
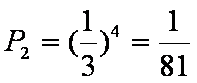
(2)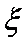
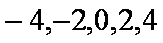
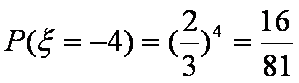
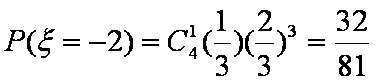
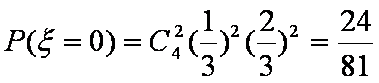
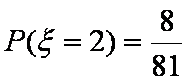

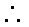
知识点
某学校为响应省政府号召,每学期派老师到各个民工子弟学校支教,以下是该学校
根据上表信息解答以下问题:
(1)从该学校任选两名老师,用





(2)从该学校任选两名老师,用


正确答案
见解析。
解析
(1) 函数


则必有

所以,
当

(2) 从该学校任选两名老师,用
则

于是


从而


知识点
扫码查看完整答案与解析