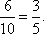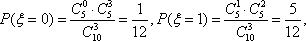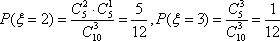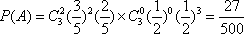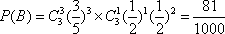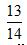- 随机事件的关系
- 共394题
一台机床有

加工B时,停机的概率是
正确答案
解析
略
知识点
下图是根据50个城市某年6月份的平均气温(单位:℃)数据得到的样本频率分布直方图,其中平均气温的范围是







正确答案
0.18;33
解析
因为



知识点
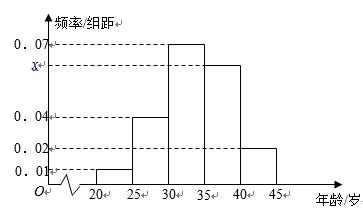
为增强市民的节能环保意识,某市面向全市征召义务宣传志愿者,从符合条件的500名志愿者中随机抽取100名志愿者,其年龄频率分布直方图如图所示,其中年龄分组区间是: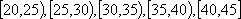
(1)求图中
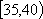
(2)在抽出的100名志愿者中按年龄采用分层抽样的方法抽取20名参加中心广场的宣传活动,再从这20名中采用简单随机抽样方法选取3名志愿者担任主要负责人,记这3名志愿者中“年龄低于35岁”的人数为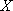
正确答案
见解析
解析
(1)∵小矩形的面积等于频率,∴除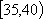
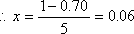
500名志愿者中,年龄在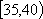
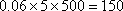
(2)用分层抽样的方法,从中选取20名,则其中年龄“低于35岁”的人有12名,
“年龄不低于35岁”的人有8名。
故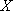
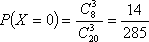
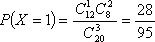
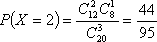

故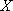
所以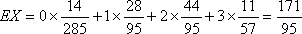
知识点
为了解甲、乙两厂的产品的质量,从两厂生产的产品中随机抽取各10件,测量产品中某种元素的含量(单位:毫克).下表是测量数据的茎叶图:
规定:当产品中的此种元素含量满足≥18毫克时,该产品为优等品.
(1)试用上述样本数据估计甲、乙两厂生产的优等品率;
(2)从乙厂抽出的上述10件产品中,随机抽取3件,求抽到的3件产品中优等品数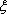
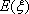
(3)从上述样品中,各随机抽取3件,逐一选取,取后有放回,求抽到的优等品数甲厂恰比乙厂多2件的概率。
正确答案
见解析
解析
(1)甲厂抽取的样本中优等品有6件,优等品率为
乙厂抽取的样本中优等品有5件,优等品率为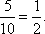
(2)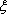
所以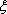
故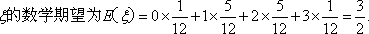
(3)抽取的优等品数甲厂恰比乙厂多2件包括2个事件,即A=“抽取的优等品数甲厂2件,乙厂0件”,B=“抽取的优等品数甲厂3件,乙厂1件”
抽取的优等品数甲厂恰比乙厂多2件的概率为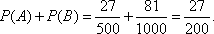
知识点
如图,三行三列的方阵中有9个数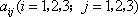

正确答案
解析
略
知识点
某工厂生产甲、乙两种产品,甲产品的一等品率为80%,二等品率为20%;乙产品的一等品率为90%,二等品率为10%.生产1件甲产品,若是一等品,则获利4万元,若是二等品,则亏损1万元;生产1件乙产品,若是一等品,则获利6万元,若是二等品,则亏损2万元。两种产品生产的质量相互独立。
(1)设生产1件甲产品和1件乙产品可获得的总利润为

(2)求生产4件甲产品所获得的利润不少于10万元的概率。
正确答案
见解析
解析
(1)由题设知,




由此得

(2)设生产的


由题设知

又


所求概率为

答:生产


知识点
某年级











正确答案
54
解析
略
知识点
某校从参加高一年级期末考试的学生中抽出60名学生,将其成绩(均为整数)分成六段


(1)求第四小组的频率,并补全这个频率分布直方图;
(2)估计这次考试的及格率(60分及以上为及格)和平均分;
(3)从成绩是70分以上(包括70分)的学生中选两人,求他们在同一分数段的概率。
正确答案
见解析。
解析
知识点
交通指数是交通拥堵指数的简称,是综合反映道路网畅通或拥堵的概念性指数值,交通指数取值范围为0~10,分为五个级别,0~2 畅 通;2~4 基本畅通;4~6 轻度拥堵;6~8 中度拥堵;8~10 严重拥堵。
早高峰时段,从北京市交通指挥中心随机选取了四环以内的50个交通路段,依据其交通指数数据绘制的直方图如图,
(1)这50个路段为中度拥堵的有多少个?
(2)据此估计,早高峰四环以内的三个路段至少有一个是严重拥堵的概率是多少?
(3)某人上班路上所用时间若畅通时为20分钟,基本畅通为30分钟,轻度拥堵为36分钟;中度拥堵为42分钟;严重拥堵为60分钟,求此人所用时间的数学期望。
正确答案
(1)18
(2)
(3)
解析
(1)
这50路段为中度拥堵的有18个。 ……………………………3分
(2)设事件A “一个路段严重拥堵”,则
事件B “至少一个路段严重拥堵”,则
所以三个路段至少有一个是严重拥堵的概率是
(3)分布列如下表:
此人经过该路段所用时间的数学期望是
知识点
已知正方形ABCD的边长为2,E、F、G、H分别是边AB、BC、CD、DA的中点。
(1)在正方形ABCD内部随机取一点P,求满足|PH|<
(2)从A、B、C、D、E、F、G、H这八个点中,随机选取两个点,记这两个点之间的 距离为ξ,求随机变量ξ的分布列与数学期望Eξ。
正确答案
见解析。
解析
(1)如图所示,正方形的面积S正方形ABCD=2×2=4。
设“满足|PH|
则S(M)=S△DGH+S△AEH+S扇形EGH=

∴ P(M)=

故满足|PH|<

(2)
从A、B、C、D、E、F、G、H这八个点中,随机选取两个点,共可得到
其中长度等于1的有8条:AE、EB、BF、FC、CG、GD、DH、HA;长度等于
FH;长度等于

∴ξ的所有可能的取值为1,


则P(ξ=1)=










随机变量ξ的分布列为
Eξ=

知识点
扫码查看完整答案与解析