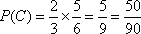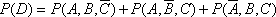- 随机事件的关系
- 共394题
某车间在三天内,每天生产10件某产品,其中第一天,第二天分别生产出了1件、

正确答案

解析
(1)


(2)由第三项的二项式系数为

知识点
从1.2.3.4.5中任取2个不同的数,事件A=“取到的2个数之和为偶数”,事件B=“取到的2个数均为偶数”,则P(B|A)=( )
正确答案
解析
事件A=“取到的2个数之和为偶数”所包含的基本事件有:(1,3)、(1,5)、(3,5)、(2,4),
事件B=“取到的2个数均为偶数”所包含的基本事件有(2,4),
知识点
如图,矩形






正确答案
解析
略
知识点
某同学参加某高校自主招生3门课程的考试。假设该同学第一门课程取得优秀成绩的概率为



(1)求该生至少有1门课程取得优秀成绩的概率及求

(2)求数学期望
正确答案
见解析。
解析
解析:用


由题意得
(1)该生至少有一门课程取得优秀成绩的概率为
(2)
及
∴
∴该生取得优秀成绩的课程门数的期望为
知识点
计算机考试分理论考试与实际操作考试两部分进行,每部分考试成绩只记“合格”与“不合格”,两部分考试都“合格”者,则计算机考试“合格”并颁发“合格证书”.甲、乙、丙三人在理论考试中“合格”的概率依次为:





(1)假设甲、乙、丙3人同时进行理论与实际操作两项考试,谁获得“合格证书”的可能性大;
(2)求这3人进行理论与实际操作两项考试后,恰有2人获得“合格证书”的概率;
(3)用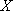
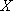
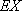
正确答案
见解析
解析
(1)记“甲获得合格证书”为事件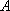
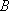
则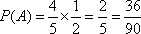
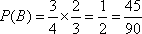
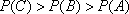
(2)设3人考试后恰有2人获得“合格证书”为事件
=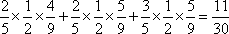
(3)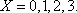
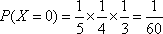
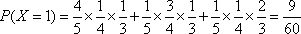
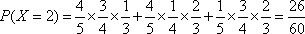
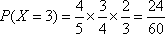
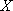
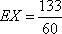
__________13分
知识点
扫码查看完整答案与解析