- 随机事件的关系
- 共394题
为了倡导健康、低碳、绿色的生活理念,某市建立了公共自行车服务系统鼓励市民租用公共自行车出行,公共自行车按每车每次的租用时间进行收费,具体收费标准如下:①租用时间不超过1小时,免费; ②租用时间为1小时以上且不超过2小时,收费1元;③租用时间为2小时以上且不超过3小时,收费2元;④租用时间超过3小时的时段,按每小时2元收费(不足1小时的部分按1小时计算)已知甲、乙两人独立出行,各租用公共自行车一次,两人租车时间都不会超过3小时,设甲、乙租用时间不超过1小时的概率分别是0.4和0.5 ,租用时间为1小时以上且不超过2小时的概率分别是0.5和0.3.(1)求甲、乙两人所付租车费相同的概率;(2)设甲、乙两人所付租车费之和为随机变量

正确答案
见解析
解析
(1)根据题意,分别记“甲所付租车费0元、1元、2元”为事件A1,A2,A3,它们彼此互斥,且
分别记“乙所付租车费0元、1元、2元”为事件B1,B2,B3,它们彼此互斥,且
由题知,A1,A2,A3与B1,B2,B3相互独立, ·············································· 3分
记甲、乙两人所付租车费相同为事件M,则M=A1B1+A2B2+A3B3,
所以P(M)=P(A1)P(B1)+ P(A2)P(B2)+ P(A3)P(B3)
=0.4×0.5+0.5×0.3+0.1×0.2=0.2+0.15+0.02=0.37;····································· 6分
(2) 据题意




······ 
······ 所以


答:甲、乙两人所付租车费相同的概率为0.37,

知识点
某超市在节日期间进行有奖促销,凡在该超市购物满300元的顾客,将获得一次摸奖机会,规则如下:
奖盒中放有除颜色外完全相同的1个红球,1个黄球,1个白球和1个黑球,顾客不放回的每次摸出1个球,若摸到黑球则停止摸奖,否则就要将奖盒中的球全部摸出才停止,规定摸到红球奖励10元,摸到白球或黄球奖励5元,摸到黑球不奖励。
(1)求1名顾客摸球3次停止摸奖的概率;
(2)记

正确答案
见解析
解析
(1)解:设“1名顾客摸球3次停止摸奖”为事件
则 
故1名顾客摸球3次停止摸奖的概率为
(2)解:随机变量






所以,随机变量
………………11分

知识点
“你低碳了吗?”这是某市为倡导建设资源节约型社会而发布的公益广告里的一句话.活动组织者为了解这则广告的宣传效果,随机抽取了
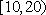
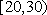

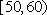
(1)求随机抽取的市民中年龄段在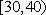
(2)从不小于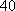

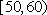
(3)从按(2)中方式得到的
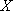
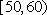
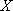
正确答案
见解析
解析
(1)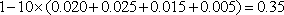
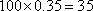
即随机抽取的市民中年龄段在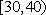
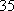
(2)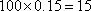
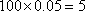
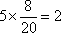
即抽取的
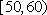
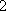
(3)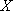

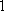
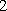
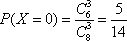
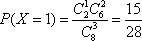
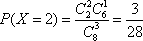
所以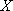
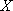
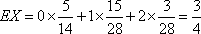
知识点
对甲、乙两名篮球运动员分别在
(1)估计甲在一场比赛中得分不低于
(2)判断甲、乙两名运动员哪个成绩更稳定;(结论不要求证明)
(3)在乙所进行的100场比赛中,按表格中各分值区间的场数分布采用分层抽样法取出10场比赛,再从这10场比赛中随机选出2场作进一步分析,记这



正确答案
见解析
解析
(1)0.72 ………2分
(2)甲更稳定, ………5分
(3)按照分层抽样法,在
内抽出的比赛场数分别 为







知识点
如图,由M到N的电路中有4个元件,分别标为T1,T2,T3,T4,电源能通过T1,T2,T3的概率都是P,电源能通过T4的概率是0.9,电源能否通过各元件相互独立,已知T1,T2,T3中至少有一个能通过电流的概率为0.999。
(1)求P;
(2)求电流能在M与N之间通过的概率。
正确答案
见解析。
解析
知识点
扫码查看完整答案与解析