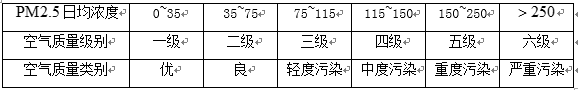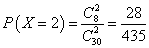- 随机事件的关系
- 共394题
设



(1)求方程
(2)求
正确答案
见解析。
解析
(1)
(2)

……1分

知识点
某大学开设甲、乙、丙三门选修课,学生是否选修哪门课互不影响. 已知某学生只选修甲的概率为0.08,只选修甲和乙的概率是0.12,至少选修一门的概率是0.88,用
(1)记“函数
(2)求的
正确答案
见解析。
解析
解析:(1)设该学生选修甲、乙、丙的概率分别为

依题意得
若函数

当


(2)依题意知
则
∴

知识点
某市地铁连同站台等附属设施全部建成后,平均每1公里需投资人民币1亿元.全部投资都从银行贷款.从投入营运那一年开始,地铁公司每年需归还银行相同数额的贷款本金0.05亿元.这笔贷款本金先用地铁营运收入支付,不足部分由市政府从公用经费中补足. 地铁投入营运后,平均每公里年营运收入(扣除日常管理费等支出后)第一年为0.0124亿元,以后每年增长20%,到第20年后不再增长.求:
(1)地铁营运几年,当年营运收入开始超过当年归还银行贷款本金?
(2)截至当年营运收入超过当年归还银行贷款本金的那一年,市政府已累计为1公里地铁支付多少元费用?(精确到元,1亿=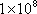
正确答案
见解析
解析
(1)地铁营运第
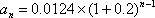
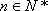
根据题意有: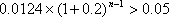
解得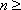
(或者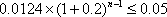
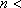
答:地铁营运9年,当年营运收入开始超过当年归还银行贷款本金. …………6分
(2)市政府各年为1公里地铁支付费用
第1年: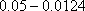
第2年: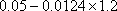
第
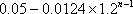

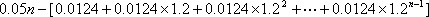
将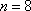
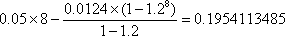
答:截至当年营运收入超过当年归还银行贷款本金的那一年,市政府累计为一公里地铁共支付19541135元费用. ………………………………………………9分
知识点
空气质量指数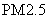
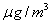
某市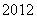
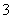
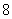
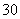
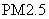
(1)估计该城市一个月内空气质量类别为良的概率;
(2)在上述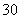
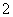
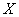
质量类别为优的天数,求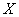
正确答案
见解析。
解析
(1)由条形统计图可知,空气质量类别为良的天数为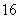
所以此次监测结果中空气质量类别为良的概率为 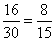
(2)随机变量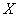
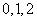
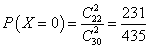
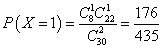
所以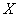
知识点
随机调查某社区

(1)将此样本的频率估计为总体的概率,随机调查



(2)根据以上数据,能否有

参考公式:

参考数据:
正确答案
见解析。
解析
(1)依题意,随机变量

方法一:





方法二:根据题意可得



(2)提出假设
根据样本提供的

因为当



知识点
扫码查看完整答案与解析