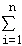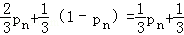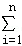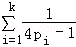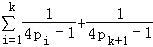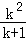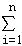- 随机事件的关系
- 共394题
某单位为绿化环境,移栽了甲、乙两种大树各




(1)求
(2)求甲种大树成活的株数大于乙种大树成活的株数的概率;
(3)用



正确答案
见解析。
解析
设“甲种大树恰有


设“乙种大树恰有


(1)两种大树各成活

(2)设“甲种大树成活的株数大于乙种大树成活的株数”为事件
则
所以,甲种大树成活的株数大于乙种大树成活的株数的概率为
(3)由题意知,

所以


知识点
中国航母“辽宁舰”是中国第一艘航母,“辽宁”号以4台蒸汽轮机为动力,为保证航母的动力安全性,科学家对蒸汽轮机进行了170余项技术改进,增加了某项新技术,该项新技术要进入试用阶段前必须对其中的三项不同指标甲、乙、丙进行通过量化检测,假如该项新技术的指标甲、乙、丙独立通过检测合格的概率分别为


(1)求该项技术量化得分不低于8分的概率;
(2)记该项新技术的三个指标中被检测合格的指标个数为随机变量X,求X的分布列与数学期望。
正确答案
见解析。
解析
(1)该项新技术的三项不同指标甲、乙、丙独立通过检测合格分别为事件


则事件“得分不低于8分”表示为

























(2)该项新技术的三个指标中被检测合格的指标个数




























随机变量






知识点
从棱长为1的正方体的8个顶点中任取不同2点,设随机变量ξ是这两点间的距离。
(1)求概率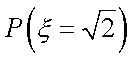
(2)求ξ的分布列,并求其数学期望E(ξ)。
正确答案
见解析。
解析
(1)从正方体的8个顶点中任取不同2点,共有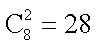
因为正方体的棱长为1,所以其面对角线长为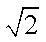
正方体每个面上均有两条对角线,所以共有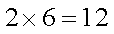
因此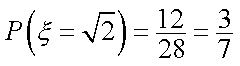
(2)随机变量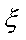
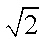
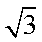
正方体的棱长为1,而正方体共有12条棱,于是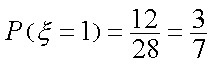
从而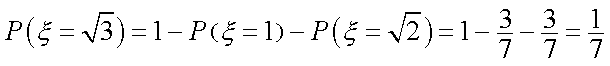
所以随机变量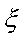
因此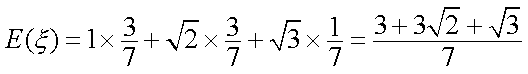
知识点
在一个盒子中有分别标有数字1,2,3,4,5的5张卡片,现从中一次取出2张卡片,则取到的卡片上的数字之积为偶数的概率是 。
正确答案
解析
从标有数字1,2,3,4,5的5张卡片中一次取出2张卡片,共有
其中取到的卡片上的数字之积为偶数分为两种情况:一类是取得的两个数字都是偶数:只有一种情况(2,4);
另一类是一个偶数和一个奇数,有
∴取到的卡片上的数字之积为偶数的概率P=
知识点
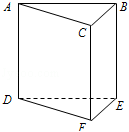
如图,一颗棋子从三棱柱的一个顶点沿棱移到相邻的另一个顶点的概率均为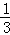
(1)求p1,p2的值;
(2)求证: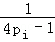
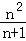
正确答案
见解析
解析
(1)棋子在上底面点A处,若移了n次后,棋子落在上底面顶点,棋子从A出发,由3条路径,所以p1=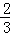
棋子移动两次,还在上底面时,有两种可能,p2=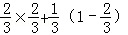
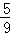
(2)因为移了n次后,棋子落在上底面顶点的概率为pn。
故落在下底面顶点的概率为1﹣pn。
于是,移了n+1次后,棋子落在上底面顶点的概率记为pn+1=
,从而pn+1﹣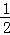
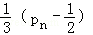
所以数列{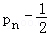
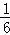
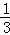
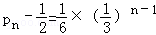
用数学归纳法证明: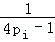
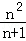
①当n=1时左式=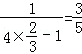
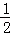
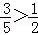
当n=2时,左式=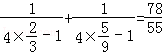
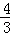
②假设n=k(k≥2)不等式成立,即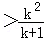
则n=k+1时,左式=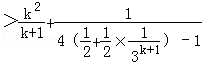
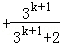
要证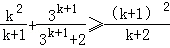
只要证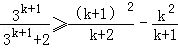
即证: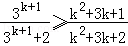
只要证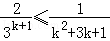
只要证3k+1≥2k2+6k+2,
因为k≥2,所以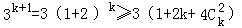
所以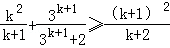
即n=k+1时不等式也成立,由①②可知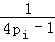
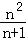
知识点
扫码查看完整答案与解析