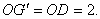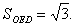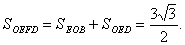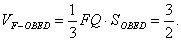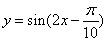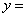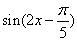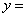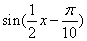- 椭圆的相关应用
- 共44题
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
函数f(x)=
正确答案
2
解析
当x≤0时,由f(x)=0得x2﹣2=0,解得x=

当x>0时,由f(x)=0得2x﹣6+lnx=0,即lnx=6﹣2x,
作出函数y=lnx和y=6﹣2x在同一坐标系图象,由图象可知此时两个函数只有1个零点,
故函数f(x)的零点个数为2
知识点
过点C(0,1)的椭圆



(1)当直线l过椭圆右焦点时,求线段CD的长;
(2)当点P异于点B时,求证:
正确答案
见解析
解析
(1)由已知得


椭圆的右焦点为







故
(2)当直线

设直线


解得


所以D点的坐标为
又直线AC的方程为

因此

所以
故
知识点
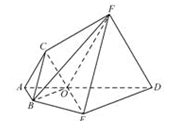
如图,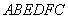
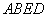
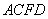
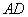
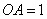
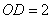
(1)证明直线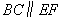
(2)求棱锥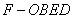
正确答案
见解析。
解析
(1)证明:设G是线段DA与EB延长线的交点. 由于△OAB与△ODE都是正三角形,所以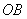
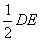
同理,设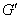
又由于G和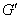
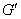
在△GED和△GFD中,由
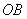
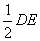
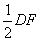
(2)解:由OB=1,OE=2,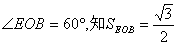
所以
过点F作FQ⊥DG,交DG于点Q,由平面ABED⊥平面ACFD知,FQ就是四棱锥F—OBED的高,且FQ=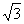
知识点
将函数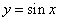

正确答案
解析
将函数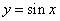
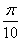
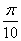
再把所得各点的横坐标伸长到原来的2倍(纵坐标不变),所得图像的函数解析式是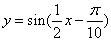
知识点
若
正确答案
解析
由于
由




知识点
i为虚数单位,(
正确答案
解析
(


知识点
设复数


正确答案
解析
知识点
在平面直角坐标系xOy中,已知椭圆C1:
(1)求椭圆C1的方程;
(2)设直线l同时与椭圆C1和抛物线C2:y2=4x相切,求直线l的方程。
正确答案
(1) 

解析
(1)由C1的左焦点F1的坐标为(-1,0)知c=1,
因为点P(0,1)在C1上,所以b=1,
于是
故C1的方程为
(2)
由题设l同时与C1和C2相切,设切点分别为A和B,点B的坐标为(x0,y0),显然x0>0,当点B在第一象限时,点B的坐标为(x0,
考虑抛物线C2在第一象限的方程

因为
所以l的斜率为

由假设直线l与椭圆C1相切,因此方程组
有唯一解,将①代入②并整理得:
(x0+2)x2+4x0x+2x0(x0-1)=0,
所以

因为x0>0,所以x0=2。
当x0=2时,直线l的方程为:
易验证l是C1的切线。
由对称性,当切点B在第四象限时,可得l的方程为:
综上所述,同时与C1和C2相切的直线方程为:

知识点
扫码查看完整答案与解析