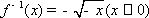- 反函数
- 共42题
函数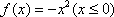


正确答案
解析
略
知识点
已知函数f(x)=ex,x∈R.
(1)若直线y=kx+1与f(x)的反函数的图像相切,求实数k的值;
(2)设x>0,讨论曲线y=f(x)与曲线y=mx2(m>0)公共点的个数;
(3)设a<b,比较

正确答案
(1) 



解析
(1)f(x)的反函数为g(x)=ln x.
设直线y=kx+1与g(x)=ln x的图像在P(x0,y0)处相切,
则有y0=kx0+1=ln x0,k=g′(x0)=
解得x0=e2,
(2)
曲线y=ex与y=mx2的公共点个数等于曲线
令

∴φ′(2)=0.
当x∈(0,2)时,φ′(x)<0,φ(x)在(0,2)上单调递减;
当x∈(2,+∞)时,φ′(x)>0,φ(x)在(2,+∞)上单调递增,
∴φ(x)在(0,+∞)上的最小值为
当0<m<

当

当


综上所述,当x>0时,
若0<m<
若
若
(3)解法一:可以证明
事实上,

令
则
∴ψ(x)在[0,+∞)上单调递增,
∴x>0时,ψ(x)>ψ(0)=0.
令x=b-a,即得(*)式,结论得证。
解法二:
=
=
设函数u(x)=xex+x-2ex+2(x≥0),
则u′(x)=ex+xex+1-2ex,
令h(x)=u′(x),则h′(x)=ex+ex+xex-2ex=xex≥0(仅当x=0时等号成立),
∴u′(x)单调递增,
∴当x>0时,u′(x)>u′(0)=0,
∴u(x)单调递增。
当x>0时,u(x)>u(0)=0.
令x=b-a,则得(b-a)eb-a+(b-a)-2eb-a+2>0,
∴
因此,
知识点
函数

正确答案


解析


知识点
在同一直角坐标系中,函数

正确答案
解析
函数

知识点
函数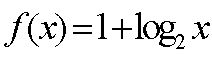
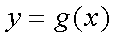
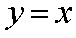
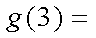
正确答案
4
解析
由已知可知g(x)与f(x)是互为反函数,设g(3)=b,则1+log2b=3,解得b=4,所以g(3)=4.
知识点
扫码查看完整答案与解析