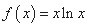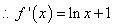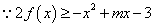- 利用导数证明不等式
- 共265题
已知函数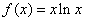
(1)求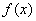
(2)若对任意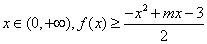
正确答案
见解析。
解析
(1) 
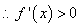
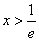

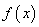
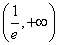
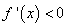
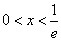

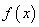
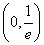

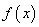
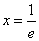
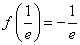
(2)
即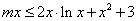
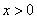
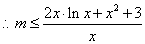
令

令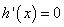
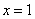
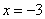
当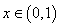
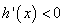
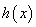
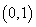
当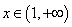
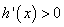
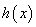
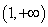
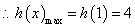
即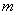
知识点
已知函数
(1)求
(2)当

正确答案
见解析
解析
(1) 定义域为

令



--------------------------------5分
所以


(2) 证明1:
设




所以


所以,当

所以

所以,当

证明2:
令

令



---------------------10分


当

故
即当

知识点
函数



正确答案
解析
略
知识点
已知函数

(1)求

(2)若锐角

正确答案
见解析
解析
知识点
已知函数


(1)求函数
(2)将函数





正确答案
见解析。
解析
(1)由题意得

由周期为


由正弦函数的单调增区间得

所以函数

(2)将函数

得到

令


所以函数在每个周期上恰有两个零点,





知识点
扫码查看完整答案与解析