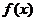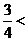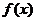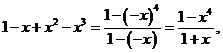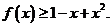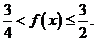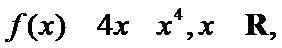- 利用导数证明不等式
- 共265题
5.函数y=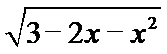
正确答案
[-3,1]
知识点
10.如图,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的表面积为()
正确答案
知识点
8.已知函数




正确答案
知识点
20.(本题满分15分)设函数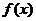
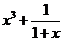
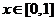
(I)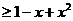
(II)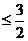
正确答案
(Ⅰ)因为
由于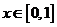
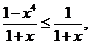
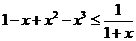
所以
(Ⅱ)由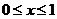
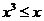
故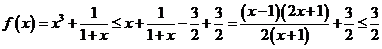
所以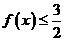
由(Ⅰ)得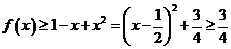
又因为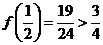
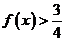
综上,
知识点
设函数
(I)求曲线

(II)设

(III)求证:

正确答案
解:(I)由

因为

所以曲线


(II)当

所以
令













由


(III)当


此时函数


当


当



当



所以
综上所述,若函数

故

当



所以

因此

知识点
6.已知





正确答案
知识点
5.一个由半球和四棱锥组成的几何体,其三视图如图所示.则该几何体的体积为
正确答案
知识点
21.
设函数
(I)讨论
(II)证明当

(III)设


正确答案
(Ⅰ)由题设,




当





(Ⅱ)由(Ⅰ)知,


所以当

故当



(Ⅲ)由题设



解得
当





由(Ⅱ)知,




所以当

知识点
23. (本题满分18分)本题共有3个小题,第1小题满分4分,第2小题满分6分,第3小题满分8分
已知


(1)当 

(2)若关于



(3)设




正确答案
(1)由

解得
(2)
等价于

当

当


综上,

(3)当


所以

函数






因为



有最小值


故

知识点
已知函数
26.求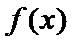
27.设曲线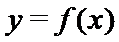
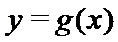
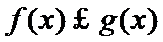
28.若方程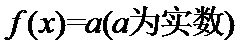
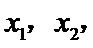
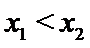
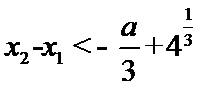
正确答案
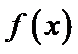
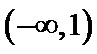
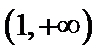
解析
试题分析:由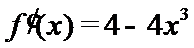
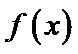
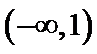
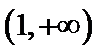
由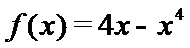
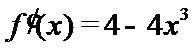
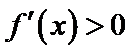
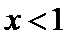
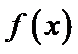
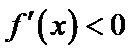
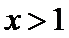
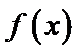
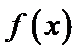
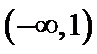
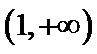
考查方向
解题思路
给出可导函数求单调区间,实质是解关于导函数的不等式,若函数解析式中不含参数,一般比较容易.不过要注意求单调区间,要注意定义域优先原则,且结果必须写成区间形式,不能写成不等式形式.
易错点
导数函数性质与原函数单调性的关系.
正确答案
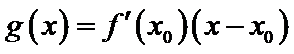
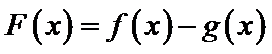
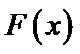
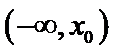
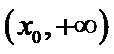
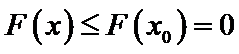
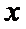
设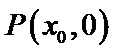
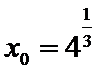
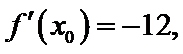
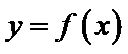
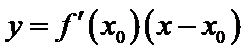
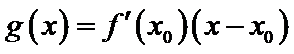
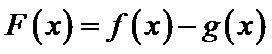
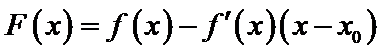
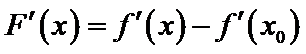
由于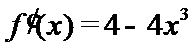
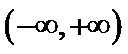
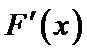
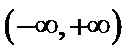
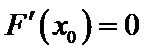
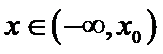
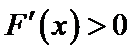
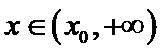
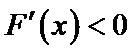
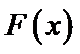
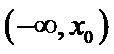
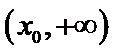
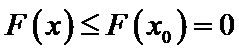
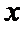
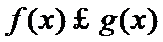
解析
见答案.
考查方向
解题思路
利用导数证明不等式是近几年高考的一个热点,解决此类问题的基本思路是构造适当的函数,利用导数研究函数的单调性和极值破解.
易错点
构造函数的性质与所求问题的联系
正确答案
设方程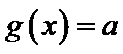
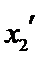
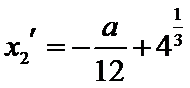
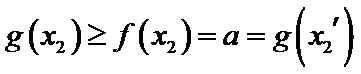
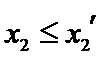
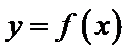
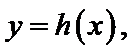
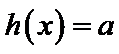
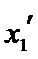
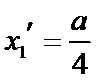
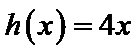
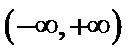
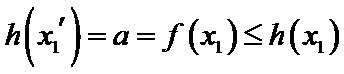
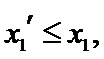
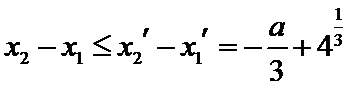
由(II)知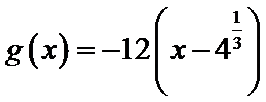
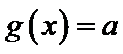
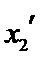
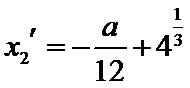
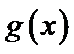
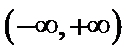
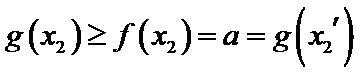
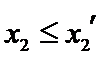
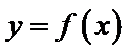
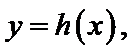
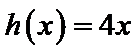
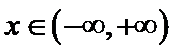
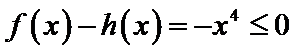
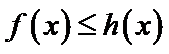
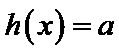
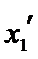
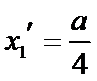
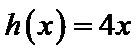
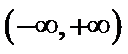
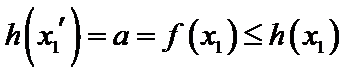
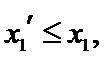
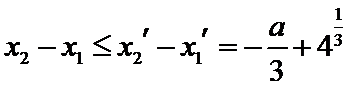
解析
见答案.
考查方向
解题思路
利用导数证明不等式是近几年高考的一个热点,解决此类问题的基本思路是构造适当的函数,利用导数研究函数的单调性和极值破解.
易错点
导数的几何意义及导函数与原函数之间的联系
扫码查看完整答案与解析