- 利用导数证明不等式
- 共265题
21.已知函数
(1)当




(2)设函数




正确答案
(1)

解析
试题分析:本题属于函数与导数的问题,
(1)直接按照步骤来求;
(2)求参数的范围的时候不会将其转化为求最值来解决。
(1)
设



(2)设




所以
由条件知
当


综上,
考查方向
解题思路
本题考查函数与导数,解题步骤如下:
(1)直接按照步骤来求;
(2)求参数的范围的时候不会将其转化为求最值来解决。
易错点
在求参数的范围的时候不会将转化为求最值来解决。
知识点
21. 已知函数

(Ⅰ)当

(Ⅱ)若关于


正确答案
(1)由



由




解析
试题分析:本题属于函数与导数的问题,(1)对函数求导,求出单调区间和极值(2)分离参数法,构造函数转化为求函数的最值.
(Ⅰ)解: 

令





由




法一(Ⅱ)令
所以





又因为
所以关于



令





因此函数




令

又因为



所以整数


令





故存在





当




所以整数
考查方向
解题思路
本题考查函数与导数的问题,解题步骤如下:
对函数求导,求出单调区间和极值。
分离参数法,构造函数转化为求函数的最值。
易错点
不会把求参数的问题转化为求函数的最值来解答。
知识点
已知函数
26.若曲线



27.若


正确答案
(1)



解析
(1) 由已知得

而



则

那么






由


考查方向
解题思路
直接利用求导,导数的几何意义直接得到所求的切线方程;后得到
易错点
求函数的单调区间时不注意定义域出错;
正确答案
(2)
解析
(2)若

即

设












从而实数
考查方向
解题思路
先分离参数后,构造函数
易错点
不会分离参数,构造函数导致无从下手。
21.已知函数
(I)求函数
(II)证明:
(III)若不等式

正确答案
见解析
解析
考查方向
解题思路
本题解题思路
1)根据共同的切线的理解得到该点处导函数值与函数值都相等得到t
2)利用单调性确定绝对值内的正负,去掉绝对值号,利用
3)构造关于m的一次函数,把x当作参数消掉m后再使用恒成立问题的解答得出结果
易错点
本题易错在以下几个方面
1)对共同的切线理解不足,第一问出错
2)使用错的解题思想
3)变量间关系不能有效理清
知识点
已知函数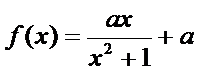

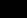
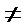
25.求函数f (x)的单调区间;
26.证明:当a > 0时,对于任意x1,x2∈(0,e],总有g(x1) < f (x2)成立,其中
正确答案
(1)当a>0时,f (x)的单调递增区间为(-1,1),单调递减区间为(-∞,-1),(1,+∞);
当a<0时,f (x)的单调递增区间为(-∞,-1),(1,+∞),单调递减区间为(-1,1);
解析
(Ⅰ)函数f (x)的定义域为R,f ′(x)=
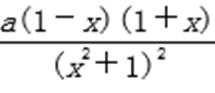
当a>0时,当x变化时,f ′(x),f(x)的变化情况如下表:
当a<0时,当x变化时,f ′(x),f(x)的变化情况如下表:
综上所述,
当a>0时,f (x)的单调递增区间为(-1,1),单调递减区间为(-∞,-1),(1,+∞);
当a<0时,f (x)的单调递增区间为(-∞,-1),(1,+∞),单调递减区间为(-1,1).
考查方向
解题思路
1)第一问对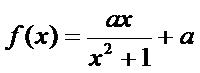
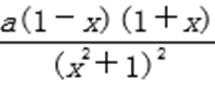
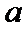
2)第二问由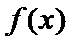
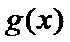
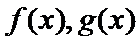
正确答案
(2)略;
解析
(Ⅱ)由(Ⅰ)可知,当a>0时,f (x)在区间(0,1)上单调递增,f (x)
f (x)在区间(1,e]上单调递减,且f (e)=
因为g(x)=aln x-x,所以g′(

①当a≥e时,g′(x)≥0在区间(0,e]上恒成立,
所以函数g(x)在区间(0,e]上单调递增,所以g(x)max=g(e)=a-e<a.
所以对于任意x1,x2∈(0,e],仍有g(x1)<f(x2).
②当0<a
因为a-(aln a-a)=a(2-ln a)>a(2-ln e)=a>0,
所以对任意x1,x2∈(0,e],总有g(x1)<f (x2).
综上所述,对于任意x1,x2∈(0,e],总有g(x1)<f (x2).
考查方向
解题思路
1)第一问对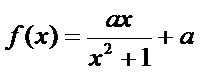
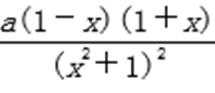

2)第二问由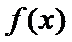
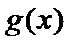
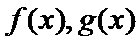
21. 设函数
(1)讨论

(2)证明:当

正确答案
(1)

当

当





当b满足0<b<




(2)由(1),可设




当

故





由于

故当

解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析













