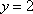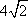- 利用导数证明不等式
- 共265题
1
题型:简答题
|
为调查民营企业的经营状况,某统计机构用分层抽样的方法从A、B、C三个城市中,抽取若干个民营企业组成样本进行深入研究,有关数据见下表:(单位:个)
(1)求

(2)若从城市A与B抽取的民营企业中再随机选2个进行跟踪式调研,求这2个都来自城市A的概率.
正确答案
见解析。
解析
(1)由题意得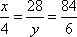
所以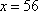
(2)记从城市A所抽取的民营企业分别为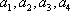
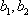
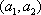

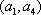
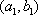
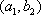
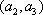
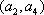
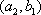
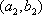
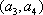
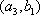

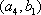
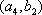

其中,来自城市A: 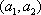
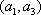
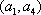
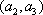
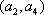

因此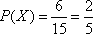

知识点
利用导数证明不等式
1
题型:填空题
|
已知在平面直角坐标系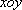


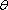
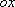
程为:
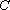
正确答案
解析
略
知识点
利用导数证明不等式
1
题型:简答题
|
已知函数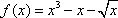
(1)判断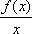
(2)求函数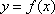
(3)令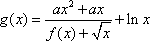
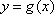

正确答案
见解析。
解析
知识点
利用导数证明不等式
1
题型:简答题
|
已知函数
(1)当


(2)求
正确答案
见解析。
解析
(1)当

又
所以
即

(2)因为
所以
(1)当
因为



所以


(2)当
令

所以当


所以当


综上,当






知识点
利用导数证明不等式
1
题型:
单选题
|
已知


正确答案
D
解析
略
知识点
利用导数证明不等式
下一知识点 : 利用导数求参数的取值范围
扫码查看完整答案与解析