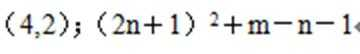- 利用导数证明不等式
- 共265题
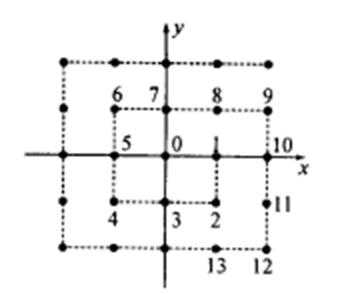
如图,将平面直角坐标系的格点(横、纵坐标均为整数的点)按如下规则标上数字标签:原点处标数字O,点(1,0)处标数字1,点(1,一1)处标数字2,点(O,-1)处标数字3,点(-1,-1)处标数字4,点(-1,0)处标数字5,点(-1,1)处标数字6,点
(0,1)处标数字7,…以此类推,①标数字50的格点的坐标为____。
②记格点坐标为(m,咒)的点(m、n均为正整数)处所标的数字为f(m,n),若n>m,则f(m,n)= ____。
正确答案
解析
f(1,0)=12,f(2,1)=32,f(3,2)=52,…,f(n+1,n)=(2n+1)2。
∵n>m,∴n≥m-1,∴当n>m时,f(m,n)=(2n+1)2+m-n-1。
知识点
若圆锥底面半径为1,高为2,则圆锥的侧面积为 。
正确答案

解析
∵圆锥的底面半径为1,高为2,
∴母线长为:
∴圆锥的侧面积为:πrl=π×1×

知识点
下列说法:
①将一组数据中的每个数据都加上或减去同一个常数后,方差恒不变;
②设有一个回归方程


③线性回归方程

④在一个
本题可以参考独立性检验临界值表
正确答案
解析
①③④正确,②回归方程


知识点
设函数
(1)当a=l时,求函数
(2)当a

(3)若对任意a∈(2,3)及任意

实数m的取值范围。
正确答案
见解析
解析
解析:(1)函数的定义域为
当

当





(2)

当


当


令
当

综上,当

当


(3)由(2)知,当

当




而

知识点
函数



正确答案
解析
由图象可知









知识点
扫码查看完整答案与解析