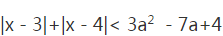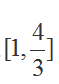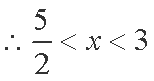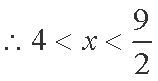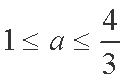- 利用导数证明不等式
- 共265题
现有在外观上没有区别的5件产品,其中3件合格,2件不合格,从中任意抽检2件,则一件合格,另一件不合格的概率为 。
正确答案
解析
从5件产品中任意抽取2有

根据古典概型的概率计算公式可得一件合格,另一件不合格的概率P=
知识点
已知函数

(1)求实数
(2)若



(3)当

正确答案
见解析
解析
(1)
令
故


(2)当

令



由于



则









(3)要证
即证 

令
又





知识点
如图,公园有一块边长为2的等边△ABC的边角地,现修成草坪,图中DE把草坪分成面积相等的两部分,D在AB上,E在AC上.
(1)设AD=x(x≥0),ED=y,求用x表示y的函数关系式;
(2)如果DE是灌溉水管,为节约成本,希望它最短,DE的位置应在哪里?如果DE是参观线路,则希望它最长,DE的位置又应在哪里?请予证明
正确答案
见解析。
解析
(1)在△ADE中,y2=x2+AE2-2x·AE·cos60°
又S△ADE=



②代入①得y2=x2+

(2)如果DE是水管y=

当且仅当x2=


如果DE是参观线路,记f(x)=x2+
函数在[1,

故f(x) max=f(1)=f(2)=5. ∴y max=
即DE为AB中线或AC中线时,DE最长.
知识点
已知

(1)讨论

(2)求证:在(1)的条件下,
(3)是否存在实数


正确答案
见解析。
解析
(1)




当



(2)



又





(3)假设存在实数

①当




解得
②当

此时
当


解得
知识点
已知关于x的不等式
(1)当a=2时,解上述不等式;
(2)如果关于x的不等式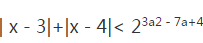
正确答案
(1)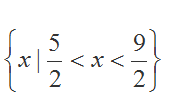
解析
解析:(1)原不等式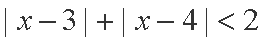
当

当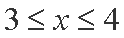
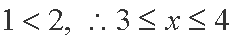
当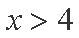
综上,原不等式解集为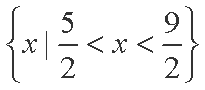
(2)
∴当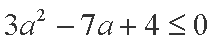
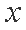
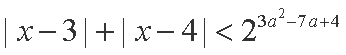
即有

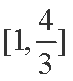
知识点
扫码查看完整答案与解析