- 与面积、体积有关的几何概型
- 共55题
7.将一颗质地均匀的骰子(一种各个面上分别标有1,2,3,4,5,6个点的正方体玩具)先后抛掷2次,则出现向上的点数之和小于10的概率是 .
正确答案
知识点
16.已知四棱锥P-ABCD的五个顶点均在同一个球面上,该四棱锥的三视图如图,则在球内任取一点Q,则点Q在四棱锥P-ABCD内的概率为_________
正确答案
解析
由三视图可知,四棱锥P-ABCD放在长方体中如图所示,
外接球的半径为R=
所以外接球的体积V球=
故所求概率P=
知识点
16.已知四棱锥P-ABCD的五个顶点均在同一个球面上,该四棱锥的三视图如图,则在球内任取一点Q,则点Q在四棱锥P-ABCD内的概率为_________
正确答案
解析
由三视图可知,四棱锥P-ABCD放在长方体中如图所示,
外接球的半径为R=
所以外接球的体积V球=
故所求概率P=
知识点
6.在边长为1的正方形ABCD内任取一点P,则动点P到点A和C的距离都小于1的概率是( )
正确答案
解析
满足条件的正方形ABCD如图所示,
其中满足条件的动点P的平面区域如图中阴影部分,
则正方形的面积S正方形=1,
阴影部分的面积S阴影=
故所求事件的概率为
知识点
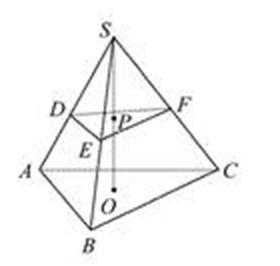
14.在三棱锥S—ABC内任取一
正确答案
解析
如图所示,只有当P点为SO的中点,即当P在三棱锥的中截面与下底面构成的三棱台内时,符合要求。所以填
考查方向
概率、三棱锥的体积的求法。
解题思路
根据题意做出图形,求解
易错点
不会计算三棱锥体积,不理解相关概率的意义
知识点
14.若不等式

正确答案
解析
由题可知SM=2π,SN=48,则P=
考查方向
本题主要考查线性规划及几何概型。
解题思路
解题步骤如下:1、画出平面区域。2、利用概率公式求解.
易错点
本题必须注意利用图像完成。
知识点
8. 在半径为2的圆内的一条直径上任取一点,过这个点作垂直该直径的弦,则弦长超过圆内接正三角形边长的概率是( )
正确答案
解析
设圆的半径为r,
圆心为O,
AB为圆的一条直径,
CD为垂直于AB的一条弦,垂足为M,
若CD为圆内接正三角形的一条边,则O到CD的距离为r/2,
设EF为与CD平行且到圆心O距离为r/2的弦,
交直径AB于点N,所以当过AB上的点且垂直于AB的弦的长度超过CD时,
该点在线段MN上移动,所以所求概率P=r/2r=1/2,所以选C
考查方向
解题思路
找到弦长于圆内接正三角形边长的情况
易错点
找临界值
知识点
13. 如图,在边长为1的正方形中随机撒1000粒豆子,有180粒落 到阴影部分,据此估计阴影部分的面积为 .
正确答案
0.18
解析
正方形的面积为1,设阴影部分的面积为S,因为随机撒1000粒豆子,有180粒落到阴影部分,所以几何概率公式进行估算:S:1=180:1000,即S=0.18,故答案为0.18
考查方向
解题思路
通过几何概率的意义计算
易错点
想不到是概率问题,用面积公式硬算
知识点
4. 如图,在边长为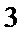
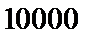
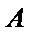
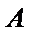
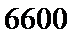
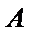
正确答案
解析
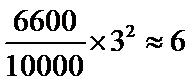
考查方向
本题考查了蒙特卡洛方法.在近几年的各省高考题出现的频率较低.
解题思路
先利用蒙特卡洛方法计算出阴影区域所占的比例,再计算阴影区域的面积.
易错点
审题失误.
知识点
14.在三棱锥S—ABC内任取一
正确答案
解析
如图所示,只有当P点为SO的中点,即当P在三棱锥的中截面与下底面构成的三棱台内时,符合要求。所以填
考查方向
概率、三棱锥的体积的求法。
易错点
不会计算三棱锥体积,不理解相关概率的意义
知识点
扫码查看完整答案与解析