抛物线的定义及应用
共118题

· 抛物线的定义及应用

抛物线的定义及应用
共118题

热门试卷

X 查看更多试卷

题型：填空题

填空题 · 5 分

抛物线的焦点坐标为

正确答案

解析

略

知识点

抛物线的定义及应用

题型：简答题

简答题 · 12 分

设抛物线C：的准线被圆O：所截得的弦长为，

（1）求抛物线C的方程

（2）设点F是抛物线C的焦点，N为抛物线C上的一动点，过N作抛物线C的切线交圆O于P、Q两点，求面积的最大值.

正确答案

见解析

解析

（1）因为抛物线C的准线方程为，且直线被圆O：所截得的弦长为，所以，解得，因此抛物线C的方程为；

（2）设N（），由于知直线PQ的方程为：. 即.

因为圆心O到直线PQ的距离为，所以|PQ|=,

设点F到直线PQ的距离为d，则，

所以，的面积S

当时取到“=”，经检验此时直线PQ与圆O相交，满足题意.综上可知，的面积的最大值为.

知识点

抛物线的定义及应用

题型：填空题

填空题 · 5 分

以抛物线y2=20x的焦点为圆心，且与双曲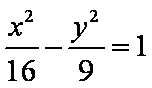的两条渐近线都相切的圆的方程为

正确答案

解析

略

知识点

抛物线的定义及应用

题型：简答题

简答题 · 12 分

已知抛物线y2=2px的焦点为F，若该抛物线上有一点A，满足直线FA的倾斜角为120°，且|FA| =4，

（1）求抛物线方程；

（2）若抛物线上另有两点B，C满足，求直线BC的方程。

正确答案

见解析

解析

（1）解：如图由AF＝4可得AM＝4，由＝1200，

可知，由抛物线的定义可得

即抛物线方程为

（2）由（1）可知点，可设点，，由可得：

，

即得，

即BC中点坐标为，而BC斜率，

所以直线BC方程为：，整理为：

知识点

抛物线的定义及应用

题型：单选题

单选题 · 5 分

已知抛物线的准线过双曲线的左焦点且与双曲线交于A、B两点，O为坐标原点，且△AOB的面积为，则双曲线的离心率为（　　）

正确答案

解析

略

知识点

抛物线的定义及应用

继续学习学习下一知识点

下一知识点 : 抛物线的标准方程和几何性质

百度题库 > 高考 > 文科数学 > 抛物线的定义及应用

扫码查看完整答案与解析