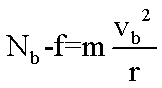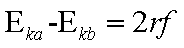- 动能定理的应用
- 共327题
山谷中有三块大石头和一根不可伸长的轻质青藤,其示意图如下。图中A、B、C、D均为石头的边缘点,O为青藤的固定点,h1=1.8m,h2=4.0m,x1=4.8m,x2=8.0m。开始时,质量分别为M=10kg和m=2kg的大、小两只滇金丝猴分别位于左边和中间的石头上,当大猴发现小猴将受到伤害时,迅速从左边石头A点起水平跳到中间石头,大猴抱起小猴跑到C点,抓住青藤的下端荡到右边石头的D点,此时速度恰好为零。运动过程中猴子均看成质点,空气阻力不计,重力加速度g=10m/s2,
求:
(1)大猴子从A点水平跳离时速度的最小值;
(2)猴子抓住青藤荡起时的速度大小;
(3)猴子荡起时,青藤对猴子的拉力大小。
正确答案
见解析。
解析
(1)根据


(2)根据机械能守恒定律得,

(3)根据牛顿第二定律得,F-(M+m)g=(M+m) 
联立解得F=216N,
知识点
如图,在:半径为2.5m的光滑圆环上切下一小段圆弧,放置于竖直平面内,两端点距最低点高度差H为1cm。将小环置于圆弧端点并从静止释放,小环运动到最低点所需的最短时间为____s,在最低点处的加速度为____m/s2。(取g=10m/s2)
正确答案
0.785 ;
0.08
解析
小环运动沿圆弧的运动可类比于单摆的简谐运动,小环运动到最低点所需的最短时间为t=T/4=




知识点
(1)我国舰载飞机在“辽宁舰”上成功着舰后,某课外活动小组对舰载飞机利用阻拦索着舰的力学问题很感兴趣。他们找来了木板、钢球、铁钉、橡皮条以及墨水,制作了如题图所示的装置,准备定量研究钢球在橡皮条阻拦下前进的距离与被阻拦前速率的关系。要达到实验目的,需直接测量的物理量是钢球由静止释放时的 和在橡皮条阻拦下前进的距离,还必须增加的一种实验器材是 。忽略钢球所受的摩擦力和空气阻力,重力加速度已知,根据 定律(定理),可得到钢球被阻拦前的速率。
(2)某同学对有故障的电热毯进行探究,题图1是电热毯的电路示意图,其中电热线和导线通过金属接线片连接。题图2为测试电路实物图,A、B为测试表笔,电压表内阻很大,可视为理想电表。
①请在答题卡虚线框内画出与题图2对应的电路图。
②断开K1,用上述测试电路在1和1′之间检测得知电热线无故障,然后测得电热线的U-I曲线如题图3所示。已知电热线材料的电阻率为2. 8×10-7 Ω·m,电热线的直径为0. 200 mm。可求得此电热线的电阻为 kΩ,总长度为 m。(结果均保留两位有效数字)
③为了进一步检查故障,该同学闭合开关K1和K2,用表笔A和B分别对题图1中所示的各点进行测试,部分测试结果如下表所示。由此测试结果可判断出电路有断路,位置在 (在“1和2”、“1′和2′”、“2和3”、“2′和3′”中选填一项)。
正确答案
(1)高度(距水平木板的高度) 刻度尺 机械能守恒(动能)
(2)①电路图(如图)
②0.58(0.57~0.59均可) 65(64~66均可)
③1′和2′
解析
(1)根据实验目的,要定量研究钢球在橡皮条阻拦下前进的距离与被阻拦前速率的关系,就需要知道这两个量的值,用刻度尺可测量钢球在橡皮条阻拦下前进的距离,根据动能定理或机械能守恒定律:mgh=
(2)①电路图如图:
②由题图可求

③由题表可知,1′和2′之间,电压表有示数,电流表示数为零,说明其间有断路。
知识点
如图,匀强电场中有一半径为r的光滑绝缘圆轨道,轨道平面与电场方向平行。a、b为轨道直径的两端,该直径与电场方向平行。一电荷为q(q>0)的质点沿轨道内侧运动.经过a点和b点时对轨道压力的大小分别为FNa和FNb不计重力,求电场强度的大小E、质点经过a点和b点时的动能。
正确答案
见解析
解析
解析:质点所受电场力的大小为f=qE,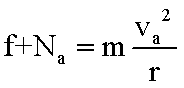
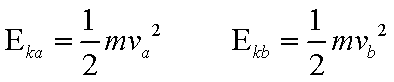
综上得: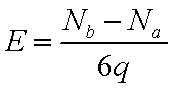
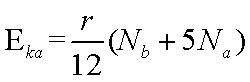
知识点
一物体放在水平地面上,如图Ⅰ所示,已知物体所受水平拉力F随时间的变化情况如图2所示,物体相应的速度
(1)0~8s时间内拉力的冲量;
(2)0~6s时间内物体的位移;
(3)0~10s时间内,物体客服摩擦力所做的功。
正确答案
见解析
解析
(1)由图2知
(2)由图3知物体的位移为
(3)由图2知,在6~8s时间内,物体作匀速运动,于是有f=2N
由图3知在0~10s时间内,物体的总位移为
所以
知识点
扫码查看完整答案与解析