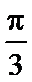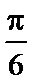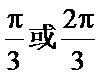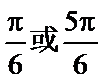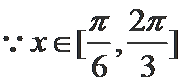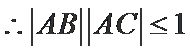- 解三角形
- 共644题
5.在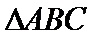
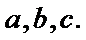
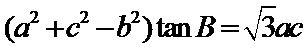
正确答案
解析
由余弦定理,知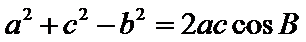
所以,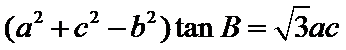
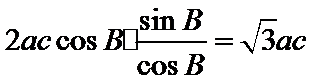
所以,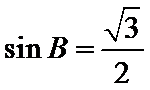
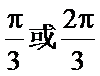
故选C。
考查方向
解题思路
由条件得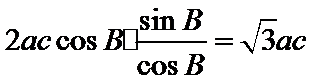
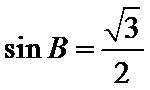
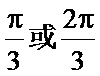
易错点
本题在把题意转化成余弦定理模型上易出错。
本题容易忽视正弦在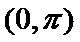
知识点
在教育宗旨问题上,梁启超主张通过教育培养
A.政治家
B.学术人才
C.新国民
D.实业人才
正确答案
C
解析
[分析] 本题旨在考查考生对中国近代维新派教育家及其代表人物教育思想贡献及其历史意义的掌握程度。维新派教育家的思想贡献在于首先明确提出普及教育的主张和培养具有时代人格精神的国民,这是他们区别于洋务派教育思想之处。尽管他们不排斥培养政治家、学术人才和实业人才,但其着眼点显然不在于此。故本题正确答案为C。
已知函数
20.求函数

21.设






正确答案
当

解析
要使





考查方向
解题思路
解题步骤如下:
易错点
本题易在利用倍角公式变形时发生错误 。
正确答案
解析
考查方向
解题思路
易错点
本题易在利用倍角公式变形时发生错误 。
已知向量m



20.求函数

21.设






正确答案
当

解析








考查方向
解题思路
解题步骤如下:利用向量的坐标运算、倍角公式、辅助角公式把函数



易错点
本题易在利用倍角公式变形时发生错误 。
正确答案
解析
由题意,得





考查方向
解题思路
解题步骤如下:由



易错点
本题易在利用倍角公式变形时发生错误 。
16.在






正确答案
2
解析
设AB=a,在三角形ABM中,cosA=











考查方向
解题思路
先将cosA表示为关系是AB边长的关系式,

易错点
根据提供的数据,选择正、余定理,函数的最值讨论
知识点
已知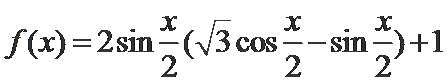
17.若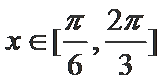
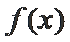

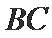
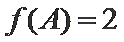
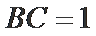
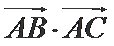
正确答案
(1)值域为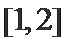
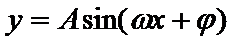
解析
(Ⅰ)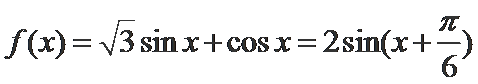

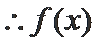
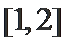
解题思路
利用降幂公式、辅助角公式把函数化成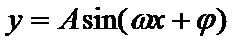
利用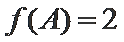
易错点
求值域时,直接带定义域的端点求最值
第2问没能联想到基本不等式求最值。
正确答案
最大值为
解析
(Ⅱ)
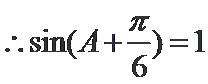
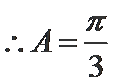
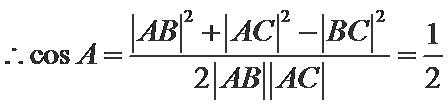
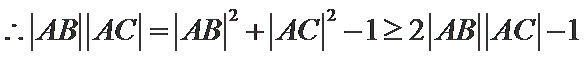
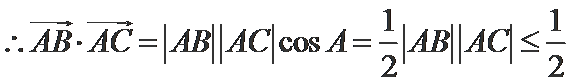
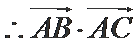
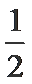
考查方向
解题思路
利用降幂公式、辅助角公式把函数化成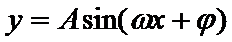
利用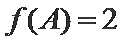
易错点
求值域时,直接带定义域的端点求最值
第2问没能联想到基本不等式求最值。
在△ABC中,已知AB=2,AC=3,A=60°.
17.求BC的长;
18.求sin2C的值.
正确答案
解析
(1)由余弦定理可得:BC2=AB2+AC2﹣2AB•ACcosA=4+8﹣2×2×3×
所以BC=
考查方向
解题思路
直接利用余弦定理求解即可。
易错点
本题考查余弦定理的应用,正弦定理的应用,在计算时易错。
正确答案
解析
由正弦定理可得:



∵AB<BC,∴C为锐角,
则cosC=


因此sin2C=2sinCcosC=2×

考查方向
解题思路
利用正弦定理求出C的正弦函数值,然后利用二倍角公式求解即可.
易错点
本题考查二倍角的三角函数,在限制角的范围过程中易错。
16.在


正确答案
知识点
14.在锐角三角形ABC中,若sinA=2sinBsinC,则tanAtanBtanC的最小值是
正确答案
8
知识点
14.在锐角三角形ABC中,若sinA=2sinBsinC,则tanAtanBtanC的最小值是 。
正确答案
8
知识点
扫码查看完整答案与解析