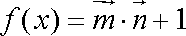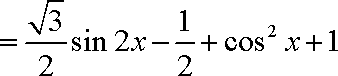- 解三角形
- 共644题
19.在一个特定时段内,以点E为中心的7海里以内海域被设为警戒水域,点E正北55海里处有一个雷达观测站A.某时刻测得一艘匀速直线行驶的船位于点A北偏东45º且与点A相距40




(1)求该船的行驶速度(单位:海里/小时)
(2)若该船不改变航行方向继续行驶,判断它是否会进入警戒水域,并说明理由.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
设函数



(1)求
(2)在








正确答案
见解析
解析
(1)

令

(2)由


∵
又∵

∴在

由

知识点
在某海岸A处,发现北偏东





正确答案
缉私船至少经过

解析
设缉私船至少经过t h 可以在D点追上走私船,则

在△ABC中,由余弦定理得,


由正弦定理得,
∴

∴点B在C的正东方向上, 
又在△DBC中,由正弦定理得
∴

∴



又
故缉私船至少经过

知识点
设函数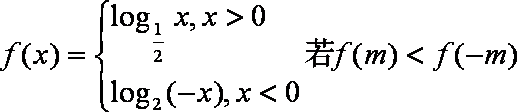
正确答案
解析
当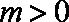
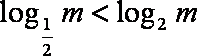
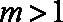
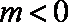
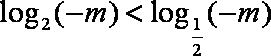
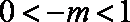
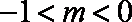
知识点
已知向量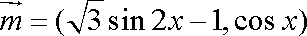
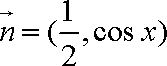
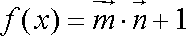
(1)求函数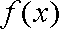
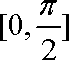
(2)已知在
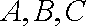
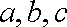
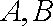
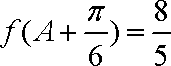
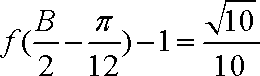
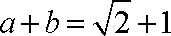
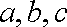
正确答案
见解析
解析
(1)函数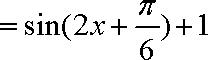
∴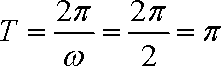
∵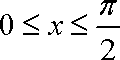
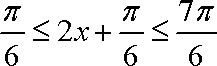
∴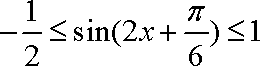
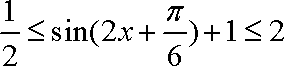
∴函数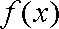
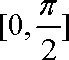
(2)∵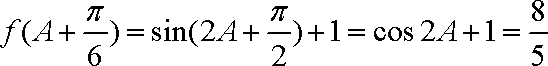
∴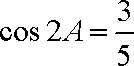
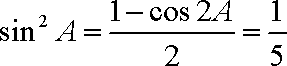
∵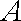
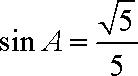
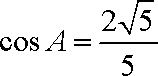
又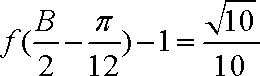
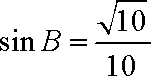
∵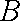
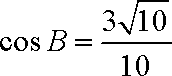
由正弦定理得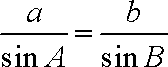
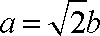
又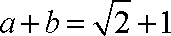
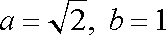
而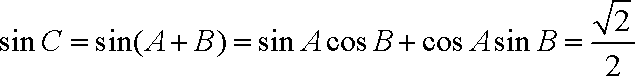
由正弦定理得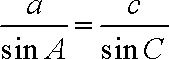
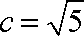
知识点
16.定义一种运算:









(1) 若

(2) 若


正确答案
29 ; 2m+3
解析
解析已在路上飞奔,马上就到!
知识点
10. 一艘海轮从A处出发,以每小时40n mile的速度沿东偏南50°方向直线航行,30min后到达B处,在C处有一座灯塔,海轮在A处观察灯塔,其方向是东偏南20°,在B处观察灯塔,其方向是北偏东65°,那么B、C两点间的距离是( )
正确答案
解析
知识点
4.某观察站









正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.如图,某观测站C在城A的南偏西

正确答案
解:在


所以
在

所以
由正弦定理

故这时此车距离A城15千米
解析
解析已在路上飞奔,马上就到!
知识点
12.将边长为1正三角形薄片,沿一条平行于底边的直线剪成两块,其中一块是梯形,记

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析