- 解三角形
- 共644题
20.已知数列{an}的首项a1=a,Sn是数列{an}的前n项和,且满足:S=3n2an+S,an≠0,n≥2,n∈N*
(1)若数列{an}是等差数列,求a的值;
(2)确定a的取值集合M,使aM时,数列{an}是递增数列。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.在
(I)求
(II)设AC=

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.在



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.底面边长为2m,高为1m的正三棱锥的全面积为( )m2
正确答案

解析
解析已在路上飞奔,马上就到!
知识点
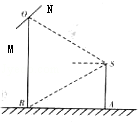
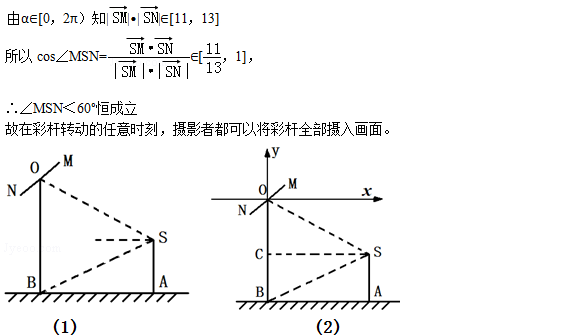
17.如图,2012年春节,摄影爱好者S在某公园A处,发现正前方B处有一立柱,测得立柱顶端O的仰角和立柱底部B的俯角均为30°,已知S的身高约为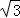
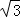
(1)求摄影者到立柱的水平距离和立柱的高度;
(2)立柱的顶端有一长2米的彩杆MN绕中点O在S与立柱所在的平面内旋转。摄影者有一视角范围为60°的镜头,在彩杆转动的任意时刻,摄影者是否都可以将彩杆全部摄入画面?说明理由。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.已知f(x)是定义在R上的可导函数,f'(x)为f(x)的导函数,又有两个向量m=(f(x),-1),n=(1,f'(x)),且对于x∈R,两向量m,n的夹角范围都是[0,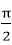
正确答案
解析
因为向量m,n的夹角范围都是[0,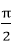
所以m·n=(f(x),-1)·(1,f'(x))=f(x)-f'(x)>0,
令F(x)=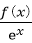
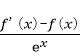
所以F(x)=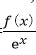
所以F(2015)<F(0),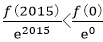
F(-2014)>F(0),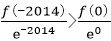
知识点
7.某船在海平面








正确答案
解析
由题可知,AB=6,AC=8.1,A=30o,可求得BC=
考查方向
本题主要考查了解三角形的实际应用举例。
解题思路
本题考查余弦定理,解题步骤如下:利用余弦定理求解。
易错点
本题要注意余弦定理。
知识点
15. 在

(1)求
(2)若点D在


正确答案
见解析
解析
解:如图, 设




又由正弦定理得
由题设知

在

考查方向
解题思路
(1)用余弦定理求a
(2)由正弦定理求sinB
(3)在
易错点
忽略数形结合思想在本题中的作用。
知识点
21.节能环保日益受到人们的重视,水污染治理也已成为“十三五”规划的重要议题.某地有三家工厂,分别位于矩形














(1)将

(2)试确定
正确答案
(1)

(2)点





解析
(1)由已知得
即

(2)记


解得

由于







考查方向
本题以实际问题为背景,主要考查函数解析式的构建以及函数最值的求解,考查数学建模的能力,是中档题.以实际问题为背景的生活中的优化问题,这类问题在近几年各省市的高考试卷中频频出现,是高考的热点问题.这类问题往往涉及到建立函数关系式和函数的最值,一般先设自变量、因变量,建立函数关系式,并确定其定义域,求最值时可利用三角函数的有界性、函数的单调性,也可直接利用导数求最值,要掌握求最值的方法和技巧.也注意结果应与实际情况相符合.
解题思路
先建立函数,再利用三角函数的有界性求
易错点
建立函数过程中,容易遗忘定义域,还要注意实际情况;求最值的有多种方法,还要注意结果应与实际情况相符合.
知识点
9. 在△ABC中,AB=AC,M为AC的中点,BM=
正确答案
解析
如图,设等腰三角形顶角为


所以当

考查方向
解题思路
如图,
设等腰三角形顶角为


易错点
不能选取合适的变量建立函数模型,或在复杂计算过程中出错
知识点
扫码查看完整答案与解析