热门试卷

A、万有引力提供向心力，由牛顿第二定律得：，解得，向心加速度：，地球表面的物体的向心加速度为9.8m/s2，所有卫星的轨道半径r都大于地球半径R，则所有卫星的向心加速度都小于9.8m/s2，故A正确；

B、万有引力提供向心力，由牛顿第二定律得：，解得： ，当卫星轨道半径r等于地球半径R时的线速度为7.9km/s，这是卫星的最大环绕速度，因此卫星的环绕速度不可能大于7.9km/s，故B错误；

C、只有同步卫星的周期为24h，卫星的周期可能大于24h，等于或小于24h，故C错误；

D、卫星绕地球做圆周运动，万有引力提供向心力，卫星的圆心一定在地心上，故D错误；

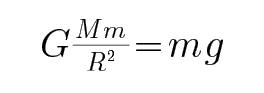
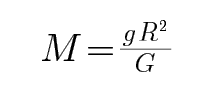
A、根据万有引力提供向心力得:，卫星质量同时出现在等号两边被约掉，可见，必须还要知道地球半径才能求出地球质量，故A错误; 

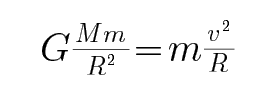
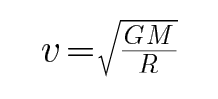
B、根据近地卫星与地球之间的万有引力提供向心力，有，解得 ，卫星质量约掉，仅知道第一宇宙速度，必须还要加上地球半径才能求出地球质量，故B错误;

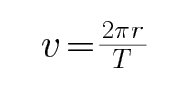
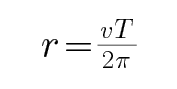
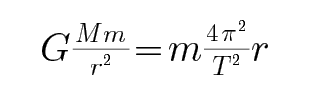
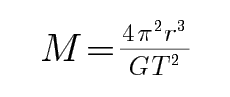
C、由得，根据万有引力提供向心力得，  解得，能求出地球质量，故C正确; 

D、中心天体是太阳，故无法求地球质量，故D错误;

A、同步轨道卫星的半径约为42400公里，是个定值，而三颗卫星的半径约为10万公里，所以这三颗卫星不是地球同步卫星，故A错误；

B、根据，得．由于三颗卫星到地球的距离相等，则它们的加速度大小相等，故B正确；

C、第一宇宙速度是绕地球运动的最大速度，则三颗卫星线速度都小于第一宇宙速度，故C错误；

D、若知道万有引力常量G及三颗卫星绕地球运转周期T可以求出地球的质量，但不知道地球半径，所以不能求出地球的密度，故D错误．

故选：B

A、卫星在椭圆轨道Q处和圆轨道Q处所受的万有引力大小相等，结合牛顿第二定律知，加速度大小相等，故A错误; 

B、在轨道A，根据万有引力提供向心力有：，在轨道B，有：，联立可以得出月球的质量和月球的半径，故B正确; 

C、卫星在轨道P处变轨时，需减速，使得万有引力大于向心力，做近心运动，故C正确; 

D、根据得，，由于卫星在轨道A上的轨道半径大于卫星在轨道B上的轨道半径，则在轨道A上的速率小于在轨道B上运动的速率，故D错误．

A、考虑了地球的自转，万有引力不等于重力，重力是万有引力的一个分力，只有两极重力才严格与万有引力相等，故A错误;

B、物体的加速度方向指向轨道的圆心，而地球上的物体随地做匀速圆周运动的轨道与地轴垂直，且维度越高轨道半径越小，只有在赤道上的物体，加速度才指向地心，故B正确; 

C、在地球上随地球自转的物体，跟随地球一起做匀速圆周运动，万有引力和支持力的合力等于向心力，万有引力沿轨道半径方向上的分力提供向心力，另一分力是重力，所以物体所受合外力不等于地球对它的万有引力，故C错误; 

D、地球表面不同纬度的物体绕同一地轴转动，角速度相等，故D错误;