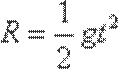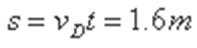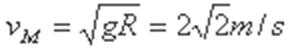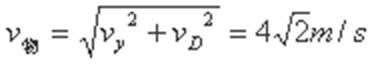- 曲线运动、万有引力
- 共1187题
16．如图，战机在斜坡上方进行投弹演练。战机水平匀速飞行，每隔相等时间释放一颗炸弹，第一颗落在a点，第二颗落在b点。斜坡上c、d两点与a、b共线，且ab=bc=cd，不计空气阻力。第三颗炸弹将落在（ ）
正确答案
解析
炸弹做平抛运动，由于落点是斜面，故飞行时间越来越长，由几何关系得第三颗炸弹将落在cd之间
考查方向
解题思路
考虑到落点是斜面，故飞行时间均匀增加
易错点
误选A
知识点
21．一个同学要研究轻弹簧的弹性势能与弹簧长度改变量的关系，进行了如下实验：在离地面高度为^的光滑水平桌面上，沿着与桌子边缘垂直的方向放置一轻质弹簧，其左端固定，右端与质量为m的一个小钢球接触。当弹簧处于自然长度时，小钢球恰好在桌子边缘，如图所示。让小钢球向左压缩弹簧一段距离后由静止释放，使钢球沿水平方向射出桌面，小钢球在空中飞行后落在水平地面上，水平距离为S。
（1）小钢球离开桌面时的速度大小为v=____________，弹簧的弹性势能Ep与小钢球质量m、桌面离地面高度h、小钢球飞行的水平距离s等物理量之间的关系式为Ep=___________。
（2）弹簧的压缩量x与对应的钢球在空中飞行的水平距离s的实验数据如下表所示：
由实验数据，可确定弹性势能Ep与弹簧的压缩量x的关系为___________（式中k为比例系数）
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
17．在水平路面上做匀速直线运动的小车上有一同定的竖直杆，其上的二个水平支架上有二个完全相同的小球A B、C,它们离地的高度分别为3h、2h和h,当小车遇到障碍物P时，立即停下来，二个小球同时从支架上水平抛出，先后落到水平路面上，如图所示。则下列说法正确的是（ ）
A二个小球落地时间差与车速有关
B三个小球落地点的间隔距离
C二个小球落地点的间隔距离
D二个小球落地点的间隔距离
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
7．一个物体做平抛运动，已知重力加速度为g。根据下列已知条件，既可以确定初速度大小，又可以确定飞行时间的是（ ）
正确答案
解析
（在每小题给出的四个选项中，有一个选项或多个选项正确。全部选对的得3分，选不全的得2分，有选错或不答的得0分）
知识点
9．2022年第24届冬季奥林匹克运动会将在北京举行，跳台滑雪是冬奥会的比赛项目之一。如图所示为一简化后的跳台滑雪的雪道示意图，运动员从O点由静止开始，在不借助其它外力的情况下，自由滑过一段圆心角为60°的光滑圆弧轨道后从A点水平飞出，然后落到斜坡上的B点。已知A点是斜坡的起点，光滑圆弧轨道半径为40m，斜坡与水平面的夹角θ＝30°，运动员的质量m＝50 kg，重力加速度g＝10 m／s2。下列说法正确的是
A运动员从O运动到B的整个过程中机械能守恒
B运动员到达A点时的速度为20 m／s
C运动员到达B点时的动能为10 kJ
D运动员从A点飞出到落到B点所用的时间为
正确答案
解析
由于从O到B过程中，只有重力在做功，故机械能守恒，A选项正确；
对OA段，由动能定理得
对AB段，水平方向：
考查方向
本题考查了平抛运动、机械能守恒定律和动能定理等
解题思路
本题中因为不涉及到重力以外的其他力的功，所以可以应用机械能守恒定律或动能定理；AB段为平抛运动，故可采取相应的公式解决。
易错点
由于忽略了圆心角60°，而由机械能守恒定律得
知识点
某新式可调火炮，水平射出的炮弹可视为平抛运动．如图，目标是一个剖面为90°的扇形山崖OAB，半径为R (R为已知) ，重力加速度为g．
11.若以初速度v0（v0为
所用时间；
12.若在同一高地P先后以不同速度射出两发炮弹，击中A点的炮弹运行的时间是击
中B点的两倍，OABP在同一竖直平面内，求高地P离A的竖直高度．
正确答案
(1) t=
解析
解析：
设炮弹质量为m，垂直击中A点时炮弹的速度方向与水平面呈45度夹角，即：
所以有：vy=v0
根据匀加速运动的公式：vy=gt
得： t=
考查方向
1、考查平抛运动的基本公式
2、考查运动的分解与合成
解题思路
1、首先分析出，炮弹垂直打在垂直打在圆弧的中点C的隐含条件
2、根据水平速度v0与竖直方向速度vy的的关系，求出竖直方向vy速度
3、根据竖直方向速度的表达式vy=gt，求出时间的表达式
易错点
容易对炮弹垂直打在垂直打在圆弧的中点C的隐含条件分析不到位
教师点评
此题主要考查学生对平抛运动中隐含条件的分析，平抛运动中多注意分析速度或位移与水平方向的夹角
正确答案
(2)h=R
5.如图所示，将小球从倾角为45。的斜面上的P点先后以不同速度向右水平抛出，分别落在斜面上的A点、B点及水平面上的C点，B点为斜面底端，P、A、B、C在水平方面间隔相等，空气阻力不计，则( )
A三次抛球，小球的飞行时间相同
B三次抛球，小球在落点处的速度方向各不相同
C先后三次抛球，抛球速度大小之比为1:2:3
D小球落在A、B两点时的速度大小之比为1:
正确答案
解析
根据h= gt2/2,由于下落的高度不同，则小球飞行时间不同，故A错误；
AB两球都落在斜面上，竖直方向的位移和水平方向上位移比值一定：tanθ=y/x=gt2/2v0t
解得：t=2v0tan45°/g．
则落在斜面上时竖直方向上的分速度vy=gt=2v0tan45°．
设速度与水平方向的夹角为α，有tanα＝vy /v0＝2tan45°＝2．
知落在斜面上时，速度与水平方向的夹角与初速度无关，则小球与水平方向的夹角相同，即小球在落点处的速度方向相同，故B错误；
若ABC三点都落在水平面上，则运动的时间相等，而P、A、B、C在水平方向间隔相等，根据v0＝x/t可知，抛球速度大小之比为1：2：3，但A不在水平面上，运动时间小于B、C两次抛出时间，故C错误；根据题意可知，小球落在A、B两点时水平位移之比为1：2，根据几何关系可知，竖直位移之比为1：2，运动时间之比为
考查方向
本题主要考查平抛运动
解题思路
解决平抛运动的方法是把平抛运动分解到水平方向和竖直方向去研究，水平方向做匀速直线运动，竖直方向做自由落体运动，平抛运动落在斜面上时，竖直方向的位移和水平方向上位移比值一定，根据该规律求出平抛运动的时间，从而求出落在斜面上时，速度与水平方向的夹角
易错点
解决本题的关键掌握平抛运动的规律，知道平抛运动在水平方向上做匀速直线运动，在竖直方向上做自由落体运动
知识点
4．如图所示，a、b的质量均为m，a从倾角为45°的光滑固定斜面顶端以初速度v0沿斜面下滑，b从斜面顶端以初速度v0平抛，不计空气阻力，则下列说法不正确的是 （ ）
正确答案
解析
对a受力分析可知，其沿光滑斜面下滑的加速度大小为：a=gsin45°，方向沿斜面向下保持不变，故做匀加速直线运动，而b物体抛出后仅受重力，做平抛运动，为匀变速曲线运动，故A选项内容正确，但不选；由机械能守恒定律可知无论是a还是b，从开始运动至落地前瞬间均有
考查方向
本题考查平抛运动及功和功率基本概念。
解题思路
1、无论是a还是b，在运动的过程中始终只有重力做功，机械能守恒，可求a、b落地的瞬时速率；
2、瞬时功率的计算为P=Fvcosθ，其中θ为F与速度v正方向间夹角。3、平均功率：
易错点
1、匀变速运动不一定是匀变速直线运动，也可以是匀变速曲线运动；
2、题干要求选择不正确的选项，审题不细导致失分。
知识点
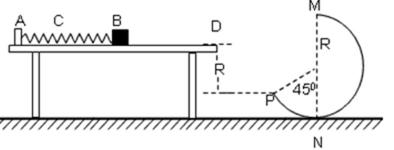
24、如图所示，水平桌面上有一轻弹簧，左端固定在A点，自然状态时其右端位于B点。水平桌面右侧有一竖直放置的光滑轨道MNP，其形状为半径R=0.8m的圆环剪去了左上角135°的圆弧，MN为其竖直直径，P点到桌面的竖直距离也是R。用质量m1=0.4kg的物块将弹簧缓慢压缩到C点，释放后弹簧恢复原长时物块恰停止在B点。用同种材料、质量为m2=0.2kg的物块将弹簧缓慢压缩到C点释放，物块过B点后其位移与时间的关系为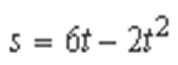
正确答案
见解析
解析
解：
（1）
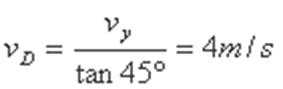
（2）若物块能过最高点，其在M点的速度至少为
设物块在P点的速度至少为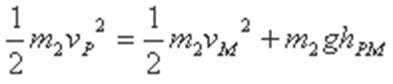
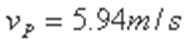
在P点时物块的速度
因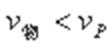
（3）设弹簧长为AC时的弹性势能为EP，物块与桌面间的动摩擦因数为μ 释放m1时，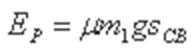
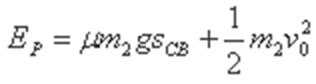
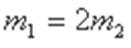
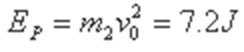
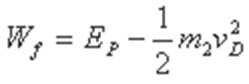
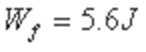
考查方向
本题主要考查平抛运动，圆周运动，机械能守恒，动能定理
解题思路
分析物体不同阶段对应的运动过程，利用相应的规律求解
易错点
摩擦力做功的问题
知识点
正确答案
解析
AB、物体在抵达斜面之前做平抛运动，加速度为g．在斜面上运动时，由牛顿第二定律得：加速度为 a= mgsinα/m=gsinα，（α是斜面的倾角），可知小球在斜面上运动的加速度大小比平抛运动时的小，故A错误，B正确．整个过程中，小球的机械能守恒，由机械能守恒定律得
考查方向
本题主要考查平抛运动
解题思路
物体在抵达斜面之前做平抛运动，加速度为g．在斜面上运动时，由牛顿第二定律求加速度．落地速率根据机械能守恒定律分析．根据位移时间公式分析落地时间关系
易错点
抓住斜面上加速度与平抛运动的加速度不同的，运用运动的分解法研究两种情况下竖直分加速度的关系，来判断落地时间的关系
知识点
扫码查看完整答案与解析