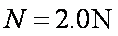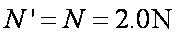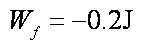- 曲线运动、万有引力
- 共1187题
如图所示,质量M=2kg的滑块套在光滑的水平轨道上,质量m=1kg的小球通过长L=0.5m的轻质细杆与滑块上的光滑轴O连接,小球和轻杆可在竖直平面内绕O轴自由转动,开始轻杆处于水平状态,现给小球一个竖直向上的初速度v0=4 m/s,g取10m/s2。
(1)若锁定滑块,试求小球通过最高点P时对轻杆的作用力大小和方向;
(2)在满足(1)的条件下,小球在最高点P突然离开轻杆沿水平方向飞出,试求小球落到水平轨道位置到轴O的距离;
(3)若解除对滑块的锁定,小球通过最高点时的速度大小v′=2m/s,试求此时滑块的速度大小。
正确答案
(1)小球对轻杆的作用力大小为2N,方向竖直向上
(2)
(3)v =1m/s
解析
(1)设小球能通过最高点,且此时的速度为v1。在上升过程中,因只有重力做功,小球的机械能守恒。则
得
设小球到达最高点时,轻杆对小球的作用力为F,方向向下,则
得F=2N
由牛顿第三定律可知,小球对轻杆的作用力大小为2N,方向竖直向上
(2)小球飞出后做平抛运动,设运动时间为t
由
到轴O的距离
得
(3)解除锁定后,设小球通过最高点时的速度为v2。
在上升过程中,系统的机械能守恒,则
得v =1m/s
知识点
一质量M=0.8kg的小物块,用长l=0.8m的细绳悬挂在天花板上,处于静止状态。一质量m=0.2kg的粘性小球以速度v0=10m/s水平射向物块,并与物块粘在一起,小球与物块相互作用时间极短可以忽略。不计空气阻力,重力加速度g取10m/s2。
求:
(1)小球粘在物块上的瞬间,小球和物块共同速度的大小;
(2)小球和物块摆动过程中,细绳拉力的最大值;
(3)小球和物块摆动过程中所能达到的最大高度。
正确答案
见解析。
解析
(1)因为小球与物块相互作用时间极短,所以小球和物块组成的系统动量守恒。
(2)小球和物块将以v共开始运动时,轻绳受到的拉力最大,设最大拉力为F,
F=15N
(3)小球和物块将以v共为初速度向右摆动,摆动过程中只有重力做功,所以机械能守恒;设它们所能达到的最大高度为h,根据机械能守恒定律:
h=0.2m
知识点
公路急转弯处通常是交通事故多发地带。如图,某公路急转弯处是一圆弧,当汽车行驶的速率为
正确答案
解析
略。
知识点
如图所示,轻线一端系一质量为m的小球,另一端套在图钉A上,此时小球在光滑的水平平台上做半径为a、角速度为ω的匀速圆周运动。现拔掉图钉A让小球飞出,此后细绳又被A正上方距A高为h的图钉B套住,达到稳定后,小球又在平台上做匀速圆周运动。求:
(1)图钉A拔掉前,轻线对小球的拉力大小;
(2)从拔掉图钉A到被图钉B套住前小球做什么运动?所用的时间为多少?
(3)小球最后做圆周运动的角速度。
正确答案
见解析
解析
(1)图钉A拔掉前,轻线的拉力大小为
(2)小球沿切线方向飞出做匀速直线运动直到线环被图钉B套住,小球速度为v=ωa,匀速运动的位移
则时间
(3)v可分解为切向速度v1和法向速度v2,绳被拉紧后v2=0,小球以速度v1做匀速圆周运动,半径r=a+h
由
得
知识点
如图所示,固定的光滑平台上固定有光滑的半圆轨道,轨道半径R=0.6m。平台上静止着两个滑块A、B,mA=0.1Kg,mB=0.2Kg,两滑块间夹有少量炸药,平台右侧有一带挡板的小车,静止在光滑的水平地面上。小车质量为M=0.3Kg,车面与平台的台面等高,车面左侧粗糙部分长度为L=0.8m,动摩擦因数为μ=0.2,右侧拴接一轻质弹簧,弹簧自然长度所在处车面光滑。点燃炸药后,A滑块到达轨道最高点时对轨道的压力大小恰好等于A滑块的重力,滑块B冲上小车。两滑块都可以看作质点,炸药的质量忽略不计,爆炸的时间极短,爆炸后两个物块的速度方向在同一水平直线上,且g=10m/s2。求:
(1)滑块在半圆轨道最低点对轨道的压力
(2)炸药爆炸后滑块B的速度大小
(3)滑块B滑上小车后的运动过程中弹簧的最大弹性势能
正确答案
见解析。
解析
(1)在最高点由牛顿第二定律:
由已知最高点压力
由机械能守恒定律:
在半圆轨道最低点由牛顿第二定律:
解得: 
由牛顿第三定律:
滑块在半圆轨道最低点对轨道的压力大小为7N,方向竖直向下 ……(1分)
(2)由动量守恒定律:

(3)由动量守恒定律:
由能量守恒定律:

知识点
如图所示,两个水平摩擦轮A和B传动时不打滑,半径
正确答案
解析
略
知识点
荡秋千是儿童喜爱的一项体育运动,当秋千荡到最高点时,小孩的加速度方向是图中的
正确答案
解析
略
知识点
山谷中有三块大石头和一根不可伸长的青之青藤,其示意图如下。图中A、B、C、D均为石头的边缘点,O为青藤的固定点,h1=1.8m,h2=4.0m,x1=4.8m,x2=8.0m。开始时,质量分别为M=10kg和m=2kg的大小两只滇金丝猴分别位于左边和中间的石头上,当大猴发现小猴将受到伤害时,迅速从左边石头A点起水平跳到中间石头,大猴抱起小猴跑到C点,抓住青藤的下端荡到右边石头的D点,此时速度恰好为零。运动过程中猴子均看成质点,空气阻力不计,重力加速度g=10m/s2,求:
(1)大猴子水平跳离的速度最小值;
(2)猴子抓住青藤荡起时的速度大小;
(3)荡起时,青藤对猴子的拉力大小。
正确答案
见解析。
解析
(1)设猴子从A点水平跳离时速的最小值为


联立①、②式,得

(2)猴子抓住青藤后的运动过程中机械能守恒,设荡起时速为


(3)设拉力为

由几何关系

得:L=10m⑧
综合⑤、⑥、⑧式并代入数据得:
知识点
如图所示,M能在水平光滑杆上自由滑动,滑杆连架装在转盘上。M用绳跨过在圆心处的光滑滑轮与另一质量为m的物体相连,当转盘以角速度
正确答案
解析
略
知识点
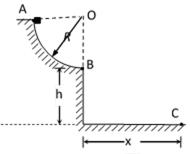
在竖直平面内有一个粗糙的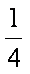
求:
(1)小滑块离开轨道时的速度大小;
(2)小滑块运动到轨道最低点时,对轨道的压力大小;
(3)小滑块在轨道上运动的过程中,克服摩擦力所做的功.
正确答案
见解析。
解析
(1)小滑块离开轨道后做平抛运动,设运动时间为t,初速度为v,则
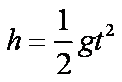
解得: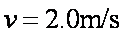
(2)小滑块到达轨道最低点时,受重力和轨道对它的弹力为N,根据牛顿第二定律: 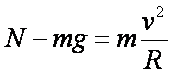
解得:
根据牛顿第三定律,轨道受到的压力大小
(3)在滑块从轨道的最高点到最低点的过程中,根据动能定理:
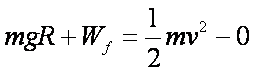
所以小滑块克服摩擦力做功为0.2J。
知识点
扫码查看完整答案与解析