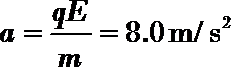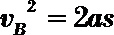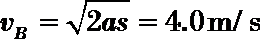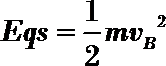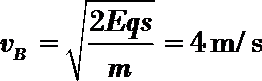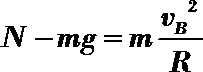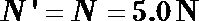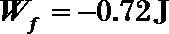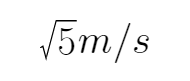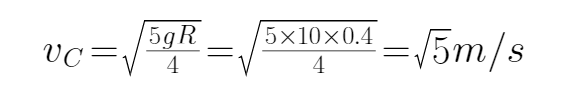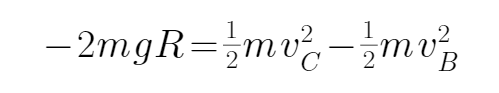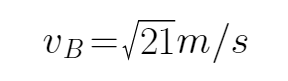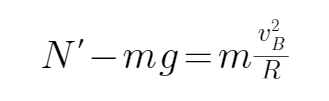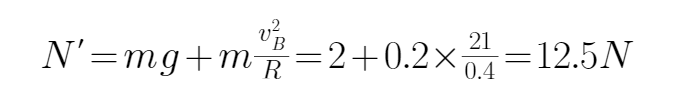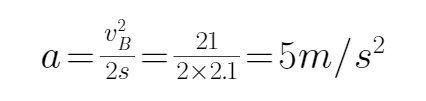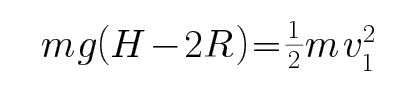- 曲线运动、万有引力
- 共1187题
18.在稳定轨道上的空间站中,物体处于完全失重状态。有如下图所示的装置,半径分别为r和R(R>r)的甲、乙两个光滑的圆形轨道安置在同一竖直平面上,轨道之间有一条水平轨道CD相通,宇航员让一小球以一定的速度先滑上甲轨道,通过粗糙的CD段,又滑上乙轨道,最后离开两圆轨道,那么下列说法正确的是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.某物理小组的同学设计了一个粗测玩具小车通过凹形桥最低点的速度的实验,所用器材有:玩具小车、压力式托盘秤、凹形桥模拟器(圆弧部分的半径为R=0.20m)。
完成下列填空:
(1)将凹形桥模拟器静置于托盘秤上,如图(a)所示,托盘秤的示数为1.00kg;将玩具小车放置在凹形桥模拟器最低点时,托盘秤示数如图(b)所示,该示数为______kg.
(2)将小车从凹形桥模拟器某一位置释放,小车经过最低点后滑向另一侧,此过程中托盘秤的最大示数为m,多次从同一位置释放小车,记录各次的m值如下表所示:
根据以上数据,可求出小车经过凹形桥最低点时对桥的压力为_______N,玩具小车通过最低点时的速度大小为_______m/s ,(重力加速度大小取9.80m/s2,计算结果保留2位有效数字)
正确答案
(1)1.40
(2)7.9;1.4
解析
解析已在路上飞奔,马上就到!
知识点
9.如图所示,甲、乙圆盘的半径之比为l:2,两水平圆盘紧靠在一起,乙靠摩擦随甲转动且不打滑。两圆盘上分别放置质量为m1和m2的小物体。己知ml=2m2,两小物体与圆盘间的动摩擦因数相同,ml距甲盘圆心的距离为r,m2距乙盘圆心的距离为2r,两小物体随盘做匀速圆周运动。下列判断正确的是( )
正确答案
解析
甲、乙两圆盘边缘上的各点线速度大小相等,有:ω1•R=ω2•2R,则得ω1:ω2=2:1,所以物块相对盘开始滑动前,m1与m2的角速度之比为ω1:ω2=2:1.根据μmg=mrω2知,μg=rω2,因为m1的轨道半径较小,则m1先达到临界角速度,可知当转速增加时,m1先开始滑动.故A正确,BCD错误
考查方向
本题主要考查向心力;线速度、角速度和周期、转速.
解题思路
当外界提供的向心力小于物体所需要的向心力时物体将做离心运动,开始滑动.根据两个转盘边缘线速度相等,分析角速度关系,再分析所需要的向心力和最大静摩擦力关系,从而作出判断
易错点
掌握向心加速度和角速度的关系公式和离心运动的条件.
知识点
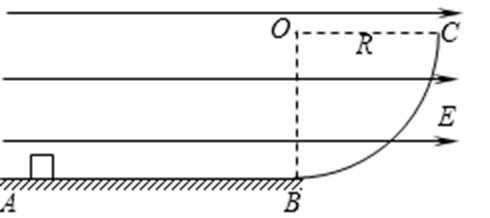
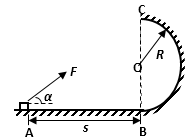
23.如图所示,绝缘光滑水平轨道AB的B端与处于竖直平面内的四分之一圆弧形粗糙绝缘轨道BC平滑连接,圆弧的半径R=0.40m。在轨道所在空间存在水平向右的匀强电场,电场强度E=1.0×104N/C。现有一质量m=0.10kg的带电体(可视为质点)放在水平轨道上与B端距离s=1.0m的位置,由于受到电场力的作用带电体由静止开始运动,当运动到圆弧形轨道的C端时,速度恰好为零。已知带电体所带电荷量q=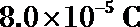
(1)带电体运动到圆弧形轨道的B端时对圆弧轨道的压力;
(2)带电体沿圆弧形轨道从B端运动到C端的过程中,摩擦力做的功。
正确答案
解:(1)设带电体在水平轨道上运动的加速度大小为a,根据牛顿第二定律有
qE =ma
解得
设带电体运动到B端的速度大小为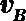
解得
(另解:由
解得
设带电体运动到圆轨道B端时受轨道的支持力为N,根据牛顿第二定律有
解得
根据牛顿第三定律可知,带电体对圆弧轨道B端的压力大小
方向:竖直向下
(2)因电场力做功与路径无关,所以带电体沿圆弧形轨道运动过程中,电场力所做的功
设带电体沿圆弧形轨道运动过程中摩擦力所做的功为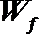
解得
解析
解析已在路上飞奔,马上就到!
知识点
12.如图所示的绝缘细杆轨道固定在竖直面内,其中,轨道半径为R的1/6圆弧段杆与水平段杆和粗糙倾斜段杆分别在A、B两点相切,圆弧杆的圆心O处固定着一个带正电的点电荷。现有一质量为m可视为质点的带负电小球穿在水平杆上,以方向水平向右、大小等于


正确答案
见解析
解析
对全过程进行受力分析,弄清楚全过程对应的运动模型,选用相应的运动规律。(1)小球从A运动到B,由动能定理得:


联立得 kQq/ R2 =mg ①
由几何关系得:OC间的距离

由①②联立解得 F=3mg/4
(3)从A到C,由动能定理得:
从C到A,由动能定理得:
据题有:



考查方向
本题主要考查机械能守恒定律,动能定理
解题思路
对全过程进行受力分析,弄清楚全过程对应的运动模型,选用相应的运动规律。
易错点
AC为圆弧,必须考虑合理提供向心力的
知识点
AB是竖直平面内的四分之一光滑圆弧轨道,在下端B与水平直轨相切,如图所示。一可视为质点的小球自A点起由静止开始沿轨道下滑。已知圆轨道半径为R,小球的质量为m,小球与水平直轨的滑动摩擦因素为µ,最终小球在C点处停住(不计空气阻力)。求:
27.小球下滑到B点时速度的大小;
28.小球经过圆弧轨道的B点和水平轨道的C点时,所受轨道支持力FB.FC各是多大?
29.BC之间的距离
正确答案

解析
根据动能定理得:
解得:
.
考查方向
动能定理
解题思路
对小球从A到B的过程运用动能定理,求出小球下滑到达B点的速度大小.
易错点
掌握动能定理的使用方法.
正确答案
(2) 

解析
小球经过圆弧轨道的B点时有:

解得:
小球在水平轨道的C点时:
考查方向
牛顿第二定律;向心力
解题思路
根据牛顿第二定律求出在B点受到的支持力大小,根据平衡求出C点受到的支持力大小.
易错点
关键分析清楚物体的运动状态:小球在B点运动状态是圆周运动,在C点是处于平衡状态.
正确答案
(3) 
解析
对全过程运用动能定理得:
小球
解得:
考查方向
动能定理
解题思路
对全过程运用动能定理,求出BC间的距离.
易错点
掌握动能定理的使用方法.
如图所示,BC为半径等于
13.O点的正上方某处A点水平抛出的初速度v0为多少?OA的距离为多少?
14.圆管中运动时对圆管的压力是多少?
15.CD斜面上运动的最大位移是多少?
正确答案
(1) 2m/s(3分) ; 0.6m(3分)
解析
(1)小球从A运动到B为平抛运动,有:
且在B点,有:
联立以上两式解得:
则,AB竖直方向的距离为:
OB竖直方向的距离为:
则,
考查方向
平抛运动
解题思路
小球从A运动到B做平抛运动,根据平抛运动的基本公式及几何关系即可求得初速度.
易错点
关键应用平抛规律解答,平抛运动水平分运动是匀速直线运动,竖直分运动是自由落体运动.
教师点评
本题考查了平抛运动,在近几年的各省高考题出现的频率较高,常与动能定理等知识点交汇命题.
正确答案

解析
在B点据平抛运动的速度规律有:
小球在管中的受力分析为三个力:由于重力与外加的力F平衡,故小球所受的合力仅为管的外轨对它的压力,得小球在管中做匀速圆周运动,由圆周运动的规律得细管对小球的作用力为:

考查方向
牛顿第二定律;牛顿第三定律;向心力
解题思路
小球从进入圆管开始受到始终竖直向上的力F=5N的作用,跟重力恰好平衡,说明小球在圆管中做匀速圆周运动,由平抛运动求出小球进入圆管时的速度,根据牛顿第二定律及第三定律求出小球对圆管的压力.
易错点
关键根据题设条件判断出小球在管中做匀速圆周运动,根据牛顿第二定律列式解答.
教师点评
本题考查了牛顿第二定律;牛顿第三定律;向心力,在近几年的各省高考题出现的频率较高,常与动能定理等知识点交汇命题.
正确答案

解析
在CD上滑行到最高点过程中,根据牛顿第二定律得:

解得:
根据速度位移关系式,得:
考查方向
牛顿第二定律;匀变速直线运动的公式
解题思路
对小球进行正确的受力分析,根据牛顿第二定律求出加速度,根据运动学公式求上滑的最大位移.
易错点
小球在粗糙的斜面上做匀减速直线运动,关键根据牛顿第二定律求出小球的加速度.
教师点评
本题考查了牛顿第二定律;匀变速直线运动的公式;向心力,在近几年的各省高考题出现的频率较高,常与动能定理等知识点交汇命题.
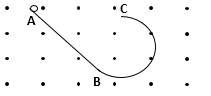
有一半径为R=0.4m的光滑半圆轨道,直径BC竖直,与粗糙水平面相切于B点,如图所示。在距B点s=2.1m的A点有一质量为m=0.2kg的小滑块,小滑块与水平面间的动摩擦因数μ = 0.5,在与水平方向成α=53º的恒力F的
26.小滑块运动到C点时速度的大小?
27.小滑块运动到圆轨道的B点,撤去F时受到轨道的支持力为多大?
28.恒力F的大小?
正确答案
解析
在C点,根据牛顿第二定律得: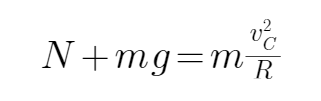
又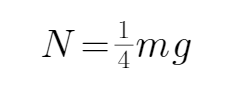
考查方向
牛顿第二定律
解题思路
根据牛顿第二定律,结合圆周运动知识,求出C点的速度.
易错点
关键对物体进行正确的受力分析,表示出C点的向心力.
教师点评
本题考查了牛顿第二定律,在近几年的各省高考题出现的频率较高,常与动能定理等知识点交汇命题.
正确答案
12.5N
解析
对B到C运用动能定理得:
代入数据解得:
根据牛顿第二定律得:
解得:
考查方向
牛顿第二定律
解题思路
根据动能定理求出B点的速度,结合牛顿第二定律求出支持力的大小.
易错点
关键求出B点的速度,由牛顿第二定律列方程.
教师点评
本题考查了牛顿第二定律,在近几年的各省高考题出现的频率较高,常与动能定理等知识点交汇命题.
正确答案
2N
解析
物块在AB段匀加速直线运动的加速度为:
根据牛顿第二定律得:Fcos53°-μ(mg-Fsin53°)=ma,
代入数据解得:F=2N.
考查方向
匀变速直线运动的公式;牛顿第二定律
解题思路
根据速度位移公式求出AB段的加速度,结合牛顿第二定律求出恒力F的大小.
易错点
理解牛顿第二定律的应用.
教师点评
本题考查了匀变速直线运动的公式;牛顿第二定律,在近几年的各省高考题出现的频率较高,常与动能定理等知识点交汇命题.
18.如图所示,在同一竖直平面内,有两个光滑绝缘的圆形轨道和倾斜轨道相切于B点,将整个装置置于垂直轨道平面向外的匀强磁场中,有一带正电小球从A处由静止释放沿轨道运动,并恰能通过圆形轨道的最高点C,现若撤去磁场,使球仍能恰好通过C点,则释放高度H’与原释放高度H的关系是( )
正确答案
解析
有磁场时,恰好通过最高点,有: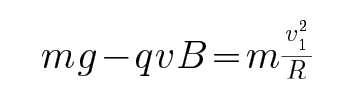
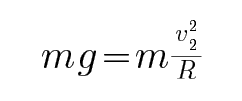
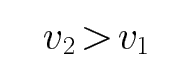
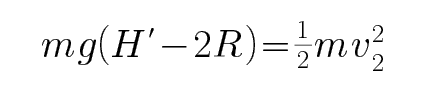
考查方向
带电粒子在匀强磁场中的运动;向心力;洛仑兹力
解题思路
有磁场时,恰好通过最高点,重力和洛伦兹力的合力提供向心力,无磁场时,恰好通过重力提供向心力,根据牛顿第二定律求出最高点的临界速度,通过动能定理比较释放点的高度.
易错点
关键理解恰好通过C时向心力的来源,明确洛伦兹力和支持力不做功.
教师点评
本题考查了带电粒子在匀强磁场中的运动,在近几年的各省高考题出现的频率较高,常与牛顿第二定律等知识点交汇命题.
知识点
如图甲,右端固定的压缩弹簧,将小球由静止弹出,小球从轨道末端A竖直飞出,恰好从转盘的M孔向上穿出,又恰好从N孔落下。已知弹簧弹性势能E=9J,小球m=0.5kg,半径为R=1m的1/4的圆轨道与水平轨道平滑连接,整条轨道的中间呈V形(如图乙),夹角为600(如图丙),圆盘匀速转动,轴与盘面垂直,孔M.N在同一直径上,且紧挨轨道上端A,不计一切摩擦.空气阻力及小球通过孔的时间,g=10m/s2,求:
24.小球在通过圆轨道上端A时,V形槽每个面对小球支持力的大小;
25.圆盘转动的最小角速度ω。
正确答案
(1)8N( 6分)
解析
由机械能守恒定律得:
解得
由牛顿第二定律得:
因V 形槽对小球的两支持力夹角为1200,
考查方向
机械能守恒定律;牛顿第二定律
解题思路
由机械能守恒定律求出经过M点的速度,再根据牛顿第二定律结合力的合成原则求解V形槽每个面对小球支持力的大小.
易错点
对小球进行正确的受力分析,由几何关系求解.
教师点评
本题考查了机械能守恒定律;牛顿第二定律,在近几年的各省高考题出现的频率较高,常与运动学等知识点交汇命题.
正确答案
(2)
解析
由运动学公式,小球离开A又回到A的时间为:
刚好从N空落下,需满足:
且
解得:
考查方向
匀速圆周运动
解题思路
由运动学公式,小球离开A又回到A的时间最短为
易错点
正确分析物体的运动情况和受力情况,理解圆盘转动时最小角速度的条件.
教师点评
本题考查了圆周运动知识点,在近几年的各省高考题出现的频率较高,常与牛顿第二定律,能量守恒等知识点交汇命题.
扫码查看完整答案与解析