不等式的性质
共451题

· 不等式的性质

不等式的性质
共451题

热门试卷

X 查看更多试卷

题型：单选题

单选题 · 5 分

6.设实数x，y满足不等式组则x2＋y2的取值范围是(　　)

A[1,2]

B[1,4]

C[，2]

D[2,4]

正确答案

解析

如图所示，不等式组表示的平面区域是△ABC的内部(含边界)，x2＋y2表示的是此区域内的点(x，y)到原点距离的平方.从图中可知最短距离为原点到直线BC的距离，其值为1；最远的距离为AO，其值为2，故x2＋y2的取值范围是[1,4].

知识点

不等式的性质

题型：填空题

填空题 · 5 分

14.若实数x，y满足，则x的取值范围是（）

正确答案

{0}[4，20]

解析

令，则a2＋b2＝x，已知条件即a2＋b2－4a－2b＝0(a≥0，b≥0)(a－2)2＋(b－1)2＝5(a≥0，b≥0)得以(2，1)为圆心，为半径，过原点的圆满足a≥0，b≥0的点.即图中及原点.x为相应点与原点距离的平方，x∈{0}∪[4，20].

知识点

不等式的性质

题型：简答题

简答题 · 15 分

20.已知函数，．

（1）当时，函数在区间上的最大值为，试求实数m的取值范围；

（2）当时，若不等式对任意（）恒成立，求实数k的取值范围．

正确答案

（1）

（2）

解析

（1）∵在上递减，在上递增，

又∵在区间上的最大值为，

∴，得，∴，即；

（2）∵ ∴恒成立

令，∴在上递增。

对于，，

知识点

不等式的性质

题型：单选题

单选题 · 5 分

11.若对，不等式恒成立，则实数的最大值是

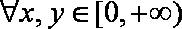
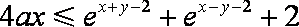
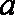
正确答案

解析

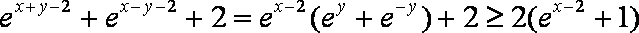
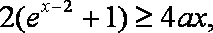
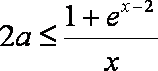
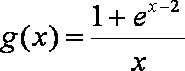
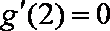
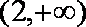
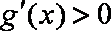
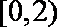
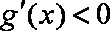
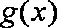
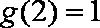
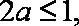
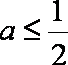
因为，再由可有，令，则，可得，且在上，在上，故的最小值为，于是即，故选D。

知识点

不等式的性质

题型：简答题

简答题 · 13 分

18.（本小题满分13分）已知函数f(x)＝ln x，.

（1）若f(x)与g(x)在x＝1处相切，求g(x)的表达式；

（2）若φ(x)＝－f(x)在[1，＋∞)上是减函数，求实数m的取值范围.

正确答案

见解析。

解析

（1）由已知得f′(x)＝，∴f′（1）＝1＝a，a＝2.

又∵g（1）＝0＝a＋b，∴b＝－1，∴g(x)＝x－1.

（2）∵φ(x)＝－f(x)＝－ln x在[1，＋∞)上是减函数.

∴φ′(x)＝≤0在[1，＋∞)上恒成立.

即x2－(2m－2)x＋1≥0在[1，＋∞)上恒成立，

则2m－2≤x＋，x∈[1，＋∞)，

∵x＋∈[2，＋∞)，∴2m－2≤2，m≤2.

故数m的取值范围是(－∞，2].

知识点

不等式的性质

继续学习学习下一知识点

下一知识点 : 不等式的应用

百度题库 > 高考 > 理科数学 > 不等式的性质

扫码查看完整答案与解析