不等式的性质
共451题

· 不等式的性质

不等式的性质
共451题

热门试卷

X 查看更多试卷

题型：简答题

简答题 · 14 分

已知函数 (a为实数)。

（1）当a=5时，求函数在x=1处的切线方程；

（2）若在区间[t，t+2](t>0)上，至少存在一个x0∈[t，t+2]，使得m>f (x0)成立。求实数m的取值范围；

（3）若存在两不等实根xl，x2∈[，e]，使方程成立，求实数a的取值范围。

正确答案

见解析。

解析

（1）当时，由得，

，故切线斜率为

所以切线方程为：

（2）根据题意大于在上的最小值即可。

①当时，在区间上为增函数，

所以

②当时，在区间上为减函数，在区间上为增函数

所以

综上，当时，；时，

（3）由得，，

令，

，，

知识点

不等式的性质

题型：填空题

填空题 · 4 分

下列正确命题的序号是____________

（1）“ ”是直线与直线相互垂直的必要不充分条件

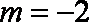
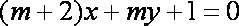
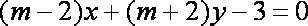
（2），使得函数是偶函数

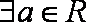
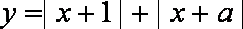
（3）不等式：≥， ≥ ，≥，…，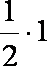

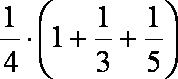
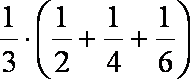
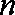
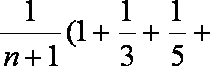
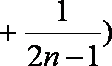
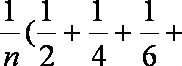
由此猜测第个不等式为…≥…

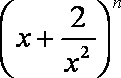
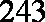
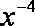
（4）若二项式的展开式中所有项的系数之和为，则展开式中的系数是

正确答案

（2）（3）

解析

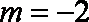
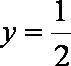
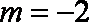
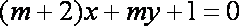
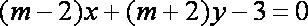
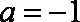
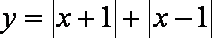
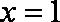
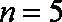
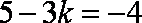
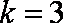
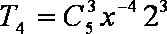
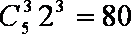
当时，两直线为和，此时两直线垂直，“ ”是直线与直线相互垂直的充分不必要条件，，所以（1）错误，所以当时，为偶函数，所以（2）正确，由归纳推理可知，（3）正确，令，则得所有项系数为，解得，二项式的通项公式为，令，得，所以，所以系数为，所以（4）错误，正确的为（2）（3）。

知识点

不等式的性质

题型：单选题

单选题 · 5 分

设变量x，y满足约束条件，则目标函数z=﹣x﹣y的取值范围是（　　）

A[-4，0]

B[-8，-2]

C[-4，-2]

D[-4，-1]

正确答案

解析

作出不等式组对应的平面区域如图：

由z=﹣x﹣y得y=﹣x﹣z，

平移直线y=﹣x﹣z，由图象可知当直线y=﹣x﹣z经过点B时，

直线的截距最大，此时z最小。

经过点A时，直线的截距最小，此时z最大。

由，解得，

即B（6，﹣2），此时zmin=﹣6﹣（﹣2）=﹣4，

由，解得，

即A（3，﹣2），此时zmax=﹣3﹣（﹣2）=﹣1，

即﹣4≤z≤﹣1，

知识点

不等式的性质

题型：简答题

简答题 · 12 分

设a∈R且a≠-,比较与-a的大小。

正确答案

见解析

解析

解: -()=,

当且时,

∵ ,

∴。

当时, ∵ ,

∴=。

当时,∵ ,

∴

知识点

不等式的性质比较法

题型：单选题

单选题 · 5 分

不等式｜x－5｜－｜x－1｜＞0的解集为

A(－，3)

B(－，－3)

C(3，＋)

D(－3，＋)

正确答案

解析

当x＝5时，｜x－5｜－｜x－1｜＝0，把｜x－5｜看到是x到5之间的距离，｜x－1｜看到成是x到1之间的距离，原不等式的几何意义就是x到5的距离与到1的距离之差大于0，画数轴可知，当x＜3时满足条件，故选A。

知识点

不等式的性质

继续学习学习下一知识点

下一知识点 : 不等式的应用

百度题库 > 高考 > 理科数学 > 不等式的性质

扫码查看完整答案与解析