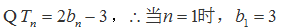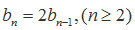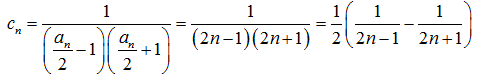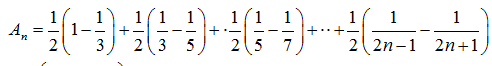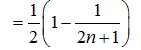- 等差数列的判断与证明
- 共87题
已知{an}是以a为首项,q为公比的等比数列,Sn为它的前n项和。
(1)当S1、S3、S4成等差数列时,求q的值;
(2)当Sm、Sn、Sl成等差数列时,求证:对任意自然数k,am+k,an+k,al+k也成等差数列。
正确答案
见解析。
解析
(1)由已知,an=aqn-1,因此S1=a,S3=a(1+q+q2),S4=a(1+q+q2+q3)。
当S1,S3,S4成等差数列时,S4-S3=S3-S1,可得aq3=aq+aq2.
化简得q2-q-1=0.解得
(2)证明:若q=1,则{an}的每项an=a,此时am+k,an+k,al+k显然构成等差数列。
若q≠1,由Sm,Sn,Sl构成等差数列可得Sm+Sl=2Sn,即
整理得qm+ql=2qn.
因此,am+k+al+k=aqk-1(qm+ql)=2aqn+k-1=2an+k,所以,am+k,an+k,al+k成等差数列。
知识点
19. 已知数列



(I)求数列
(II)令


正确答案
知识点
8.如图,点列


(P≠Q表示点P与Q不重合)
若


正确答案
知识点
18. 已知数列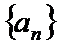
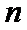
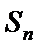
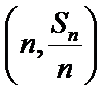
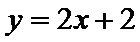
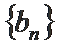
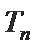
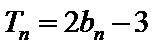
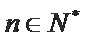
(Ⅰ)求数列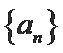
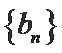
(Ⅱ)设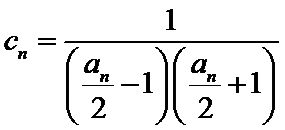
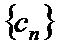
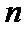
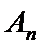
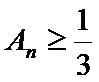
正确答案
(1)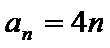
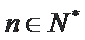
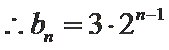
解析
试题分析:本题属于数列中的基本问题,题目的难度是逐渐由易到难.
解:(Ⅰ)由题意,得 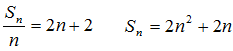
当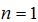
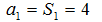
当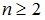
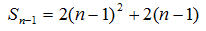
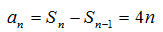
综上,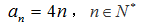
又
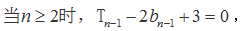
数列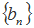
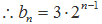
(Ⅱ)
考查方向
解题思路
本题考查数列问题,解题步骤如下:
1、利用an与Sn的关系求解。
2、利用等比数列的求和公式求解。
易错点
等比数列分项时项数易错。
知识点
18. 设数列

(1)求数列

(2)是否存在正整数n,使得
正确答案
(1)
(2)
解析
本题属于三角函数的图像与性质及正余弦定理的综合应用问题,属于简单题,只要掌握相关函数的知识,即可解决本题,解析如下:
解:(1)
所以
两式相减得:
即

所以

所以
所以
所以
所以
所以

考查方向
本题考查了数列的相关知识点,属于简单题。
易错点
相关知识点不熟悉导致出错。
知识点
扫码查看完整答案与解析