- 牛顿运动定律
- 共1024题
如图,竖直平面内的轨道I和II都由两段细直杆连接而成,两轨道长度相等。用相同的水平恒力将穿在轨道最低点B的静止小球,分别沿I和II推至最高点A,所需时间分别为t1、t2;动能增量分别为△Ek1、△Ek2,假定球在经过轨道转折点前后速度大小不变,且球与I. II轨道间的动摩擦因数相等,则
正确答案
解析
小球从最低点到最高点受到摩擦力做功:Wf=μmgcosα×L=μmgx水平与斜面倾角无关;水平拉力为恒力,水平位移相同,所以拉力做功相等,根据动能定理可知,两球到达A点时的速度相同,动能相等,AC项错误;将小球的运动看做直线运动,画出其速率随时间变化的图象,
可知,沿II轨道运动的小球先到达,B项正确。
知识点
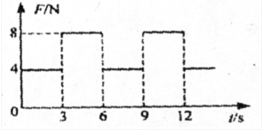
质量为2kg的物体静止在足够大的水平面上,物体与地面间的动摩擦因数为0.2,最大静摩擦力和滑动摩擦力大小视为相等。从t=0时刻开始,物体受到方向不变、大小呈周期性变化的水平拉力F的作用,F随时间t的变化规律如图所示。重力加速度g取10m/s2,则物体在t=0到t=12s这段时间内的位移大小为
正确答案
解析
拉力只有大于最大静摩擦力时,物体才会由静止开始运动。0-3s时:F=fmax,物体保持静止,s1=0;3-6s时:F>fmax,物体由静止开始做匀加速直线运动,
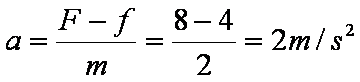
v=at=6m/s,
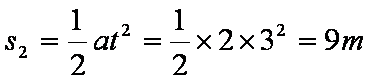
6-9s时:F=f,物体做匀速直线运动,
s3=vt=6×3=18m,
9-12s时:F>f,物体以6m/s为初速度,以2m/s2为加速度继续做匀加速直线运动,
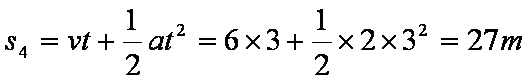
所以0-12s内物体的位移为:s=s1+s2+s3+s4=54m,B正确。
知识点
如图所示,一工件置于水平地面上,其AB段为一半径





(1)若工件固定,将物块由P点无初速度释放,滑至C点时恰好静止,求P、C两点间的高度差h。
(2)若将一水平恒力F作用于工件,使物体在P点与工件保持相对静止,一起向左做匀加速直线运动
①求F的大小
②当速度时,使工件立刻停止运动(即不考虑减速的时间和位移),物块飞离圆弧轨道落至BC段,求物块的落点与B点间的距离。
正确答案
见解析。
解析
(1)物块从P点下滑经B点至C点的整个过程,根据动能定理得

代入数据得

(2)①设物块的加速度大小为


根据牛顿第二定律,对物体有

对工件和物体整体有

联立②③④⑤式,代入数据得

②设物体平抛运动的时间为





联立②③⑦⑧⑨式,代入数据得

知识点
某校举行托乒乓球跑步比赛,赛道为水平直道,比赛距离为s.比赛时,某同学将球置于球拍中心,以大小为a的加速度从静止开始做匀加速直线运动,当速度达到v0时,再以v0做匀速直线运动跑至终点,整个过程中球一直保持在球拍中心不动,比赛中,该同学在匀速直线运动阶段保持球拍的倾角为θ0,如图所示,设球在运动中受到的空气阻力大小与其速度大小成正比,方向与运动方向相反,不计球与球拍之间的摩擦,球的质量为m,重力加速度为g.
(1)求空气阻力大小与球速大小的比例系数k;
(2)求在加速跑阶段球拍倾角θ随速度v变化的关系式;
(3)整个匀速跑阶段,若该同学速度仍为v0,而球拍的倾角比θ0大了β并保持不变,不计球在球拍上的移动引起的空气阻力变化,为保证到达终点前球不从球拍上距离中心为r的下边沿掉落,求β应满足的条件。
正确答案
见解析。
解析
(1)在匀速运动阶段,有mgtanθ0=kv0
(2)加速阶段,设球拍对球的支持力为N′,有
N′sinθ-kv=ma
N′cosθ=mg
得
(3)以速度v0匀速运动时,设空气阻力与重力的合力为F,有
球拍倾角为θ0+β时,空气阻力与重力的合力不变,设球沿球拍面下滑的加速度大小为a′,有
Fsinβ=ma′
设匀速跑阶段所用时间为t,有
球不从球拍上掉落的条件
知识点
如图所示,物体A放在足够长的木板B上,木板B静止于水平面。t=0时,电动机通过水平细绳以恒力F拉木板B,使它做初速度为零,加速度aB=1.0m/s2的匀加速直线运动。已知A的质量mA和B的质量mg均为2.0kg,A、B之间的动摩擦因数

(1)物体A刚运动时的加速度aA
(2)t=1.0s时,电动机的输出功率P;
(3)若t=1.0s时,将电动机的输出功率立即调整为P`=5W,并在以后的运动过程中始终保持这一功率不变,t=3.8s时物体A的速度为1.2m/s。则在t=1.0s到t=3.8s这段时间内木板B的位移为多少?
正确答案
见解析
解析
(1)物体

代入数据解得
(2)


木板


解得:
电动机输出功率 
(3)电动机的输出功率调整为



解得
木板

所以木板





这段时间内片的位移

由以上各式代入数据解得:
木板



知识点
如图所示,生产车间有两个相互垂直且等高的水平传送带甲和乙,甲的速度为v0。小工件离开甲前与甲的速度相同,并平稳地传到乙上,工件与乙之间的动摩擦因数为μ。 乙的宽度足够大,重力加速度为g。
(1)若乙的速度为v0,求工件在乙上侧向(垂直于乙的运动方向)滑过的距离s;
(2)若乙的速度为2v0,求工件在乙上刚停止侧向滑动时的速度大小v;
(3)保持乙的速度2v0不变,当工件在乙上刚停止滑动时, 下一只工件恰好传到乙上,如此反复。若每个工件的质量均为m,除工件与传送带之间摩擦外,其他能量损耗均不计,求驱动乙的电动机的平均输出功率P。
正确答案
答案:(1)

解析
(1)摩擦力与侧向的夹角为45°
侧向加速度大小
解得
(2)设t=0时刻摩擦力与侧向的夹角为

则
很小的

解得
且由题意可知
所以摩擦力方向保持不变
则当
即
(3)工件在乙上滑动的侧向位移为x,沿乙方向的位移为y
由题意知
在侧向上
工件滑动时间
工件相对乙的位移
则系统摩擦生热
电动机做功
由
知识点
如右图,轻弹簧上端与一质量为m的木块1相连,下端与另一质量为M的木块2相连,整个系统置于水平放置的光滑木板上,并处于静止状态。现将木板沿水平方向突然抽出,设抽出后的瞬间,木块1、2的加速度大小分别为

正确答案
解析
在抽出木板的瞬时,弹簧对1的支持力和对2的压力并未改变。对1物体受重力和支持力,mg=F,a1=0. 对2物体受重力和压力,根据牛顿第二定律
知识点
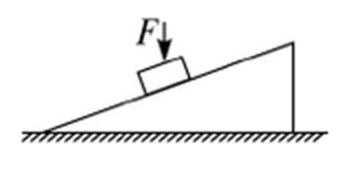
如图所示,放在固定斜面上的物块以加速度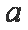
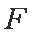
正确答案
解析
根据题意,放在斜面上的物块沿斜面以加速度a匀加速下滑,在沿斜面方向对物块由牛顿第二定律有mgsinθ-μmgcosθ=ma①,在物块上施加竖直向下的力F后,在沿斜面方向对物块由牛顿第二定律有(mg+F)sinθ-μ(mg+F)cosθ=ma0②,由①②易知a0>a,C项正确、A、B、D三项错误。
知识点
以不同初速度将
正确答案
解析
略
知识点
如图,水平地面上的矩形箱子内有一倾角为
(1)求箱子加速阶段的加速度大小a'。
(2)若a>g tan
正确答案
(1)
解析
(1)设加速过程中加速度为a‘,由匀变速运动公式
解得
(2)设球不受车厢作用,应满足
解得
减速时加速度由斜面支持力N与左壁支持力P共同决定,当
P=0
球受力如图。
由牛顿定律
解得
知识点
扫码查看完整答案与解析