- 牛顿运动定律
- 共1024题
如图2所示,一轻质弹簧其上端固定在升降机的天花板上,下端挂一小球,在升降机匀速竖直下降过程中,小球相对于升降机静止。若升降机突然停止运动,设空气阻力可忽略不计,弹簧始终在弹性限度内,且小球不会与升降机的内壁接触,则以地面为参照系,小球在继续下降的过程中 ( )
正确答案
解析
略
知识点
如图所示,粗糙水平地面AB与半径R=0.4m的光滑半圆轨道BCD相连接,且在同一竖直平面内,O是BCD的圆心,BOD在同一竖直线上。质量m=2kg的小物体在9N的水平恒力F的作用下,从A点由静止开始做匀加速直线运动。已知AB=5m,小物块与水平地面间的动摩擦因数为
求:
(1)小物块到达B点时速度的大小;
(2)小物块运动到D点时,轨道对小物块作用力的大小;
(3)小物块离开D点落到水平地面上的点与B点之间的距离。
正确答案
见解析。
解析
(1)从A到B,根据动能定理有 (

得 
(2)从B到D,根据机械能守恒定律有 
得 
在D点,根据牛顿运动定律有 
得 F= 
(3)由D点到落点小物块做平抛运动,在竖直方向有 
得 
水平面上落点与B点之间的距离为 x = vDt = 3×0.4 = 1.2m
知识点
小铁块置于长木板右端,木板放在光滑的水平地面上,t=0时使二者获得等大反向的初速度开始运动,经过时间t1铁块在木板上停止滑动,二者相对静止,此时与开始运动时的位置相比较,下图中能够反映可能发生的是( )
正确答案
解析
略
知识点
如图所示,质量为m1=lkg的小物块由静止轻轻放在水平匀速运动的传送带上,从A点随传送带运动到水平部分的最右端B点,经半圆轨道C点沿圆弧切线进入竖直光滑的半圆轨道,恰能做圆周运动。C点在B点的正上方,D点为轨道的最低点。小物块m1到达D点后与静止在D点的质量为m2=0.5kg小物块发生碰撞,碰撞后,两者均做平抛运动,m2恰好垂直于倾斜挡板打在挡板跟水平面相交的E点,m1落在F点,已知半圆轨道的半径R=0.5m,D点距水平面的高度h =0.45m,倾斜挡板与水平面之间的夹角θ=53°,不考虑空气阻力,试求:(1)摩擦力对小物块m1做的功;(2)水平面上EG间的距离;(3)小物块m1碰撞m2后经过D点时对轨道压力的大小。(题目中可能要用到的数据:g=10 m/s2,sin37°=0.6,cos37°=0.8)
正确答案
见解析。
解析
(1)设小物体m1经过C点时的速度大小为v1,因为经过C点恰能做圆周运动,
由牛顿第二定律得:


小物体m1由A到B过程中,设摩擦力对小物体做的功为Wf,由动能定理得:

(2)小物体m2离开D点后做平抛运动,设经过时间t打在E点,由

设小物体m2打在E点时速度的水平、竖直分量分别为

速度跟竖直方向的夹角为θ,则:


解得:

(3)设小物体m1经过D时的速度大小为v2,对C点运动到D点的过程,
由机械能守恒定律得: 
小物体m1经过D点时,与m2发生碰撞,由动量守恒定律可得,

设轨道对m1的支持力大小为FN,由牛顿第二定律得:

代入数据,联立解得:FN=28N,(1分)由牛顿第三定律可知,
小物体m1对轨道的压力大小为:
知识点
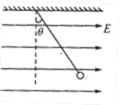
如图所示,绝缘细线下挂着一带电小球,它的质量为m,整个装置处于水平向右的匀强电场中。小球平衡时,细线与竖直方向的夹角为θ,重力加速度为g,则( )
正确答案
解析
略
知识点
如图所示,一木板放置在水平桌面上, A、B两个小物体通过不可伸长的轻绳相连,并且跨过轻滑轮,A物体放置在木板的最左端,滑轮与物体A间的细绳平行于桌面。已知木板的质量m1=20.0kg,物体A的质量m2=4.0kg,物体B的质量m3=1.0kg,物体A与木板间的动摩擦因数
(1)求力F1的大小;
(2)为了使物体A随着木板一起向左运动,并且不发生相对滑动,现把力F1替换为水平向左的力F2,求力F2的最大值;
(3)现用水平向左的力打击木板,同时撤去力F1。使物体B上升高度hB=1.0m(物体B未碰触滑轮)时,物体A刚好到达木板最右端。求打击木板的冲量大小I。
正确答案
见解析。
解析
(1)
对物体B受力分析如图1所示,
根据共点力平衡条件 T1=m3g ①
对物体A和木板组成的整体受力分析如图2所示
根据共点力平衡条件得 F1=T1 ②
代入数据,由①、②得 F1=10N
(2)
运动过程中,三个物体的加速度大小相等,设加速度大小为a。
对物体B受力分析如图3所示,
根据牛顿第二定律 T2–m3g= m3a ③
对物体A受力分析如图4所示,
根据牛顿第二定律 f–T2 = m2a ④
此时,f =μm2g ⑤
代入数据,由③、④、⑤式得
a =2.0m/s2
对木板受力分析如图5所示,
根据牛顿第二定律 F2–f= m1a ⑥
将加速度代入⑥式得 F2= 60N
(3)
由于木板与物体A之间的最大静摩擦力等于滑动摩擦力,物体A、B运动的加速度与(2)中的加速度相等。即a =2.0m/s2
设物体B上升高度hB=1.0m,所用时间为t,满足
代入数据,解得 t =1.0s
设木板减速运动过程中的加速度为
对木板受力分析如图6所示
根据牛顿第二定律
代入数据,解得
根据题意,物体B上升高度hB=1.0m过程中,
木块向左运动的位移x=L+hB=3m
设打击木板后的瞬间,木板的速度为v0,
物体A刚好到达木板最右端时,木板的速度
对木板,根据运动学公式
代入数据,解得 v0=3.5m/s
根据动量定理 I=m1v0-0
代入数据,解得 I=70N·s
知识点
“蹦极”运动是勇敢者的运动。蹦极运动员将弹性长绳(质量忽略不计)的一端系在双脚上,另一端固定在高处的跳台上,运动员无初速地从跳台上落下。若不计空气阻力,对于运动员的第一次下落过程,以下说法中正确的是 ( )
正确答案
解析
略
知识点
光滑水平面上的木块受到水平力


正确答案
解析
略
知识点
质量为10 kg的环在F=200 N的拉力作用下,沿粗糙直杆由静止开始运动,杆与水平地面的夹角θ=37°,拉力F与杆的夹角也为θ=37°。力F作用0.5s后撤去,环在杆上继续上滑了0.4s后,速度减为零。求:
(1)环与杆之间的动摩擦因数μ;
(2)环沿杆向上运动的总距离s。
正确答案
见解析
解析
物体的整个运动分为两部分,设撤去力 F 瞬间物体的速度为 v,则
由 v = a1 t1和 0 = v – a2 t2得a1 t1 = a2 t2 或2 a1 = 1.6 a2①
ma1 = F cosθ- mg sinθ-μ(F sinθ - mg cosθ)②
ma2 = mg sinθ +μmg cosθ③
由①,②,③式联立解得
μ= 0.5
代入②,③得 a1 = 8(m/s2) a2 = 10(m/s2)
s2 = 



知识点
质量为2kg的物体静止在足够大的水平



正确答案
解析
略
知识点
扫码查看完整答案与解析