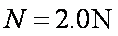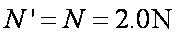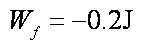- 牛顿运动定律
- 共1024题
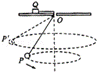
如图所示,质量M=2kg的滑块套在光滑的水平轨道上,质量m=1kg的小球通过长L=0.5m的轻质细杆与滑块上的光滑轴O连接,小球和轻杆可在竖直平面内绕O轴自由转动,开始轻杆处于水平状态,现给小球一个竖直向上的初速度v0=4 m/s,g取10m/s2。
(1)若锁定滑块,试求小球通过最高点P时对轻杆的作用力大小和方向;
(2)在满足(1)的条件下,小球在最高点P突然离开轻杆沿水平方向飞出,试求小球落到水平轨道位置到轴O的距离;
(3)若解除对滑块的锁定,小球通过最高点时的速度大小v′=2m/s,试求此时滑块的速度大小。
正确答案
(1)小球对轻杆的作用力大小为2N,方向竖直向上
(2)
(3)v =1m/s
解析
(1)设小球能通过最高点,且此时的速度为v1。在上升过程中,因只有重力做功,小球的机械能守恒。则
得
设小球到达最高点时,轻杆对小球的作用力为F,方向向下,则
得F=2N
由牛顿第三定律可知,小球对轻杆的作用力大小为2N,方向竖直向上
(2)小球飞出后做平抛运动,设运动时间为t
由
到轴O的距离
得
(3)解除锁定后,设小球通过最高点时的速度为v2。
在上升过程中,系统的机械能守恒,则
得v =1m/s
知识点
如图,光滑水平面上存在水平向右、场强为









(1) 物体
(2) 物体

(3) 弹簧的最大弹性势能。
正确答案
见解析。
解析
(1)小球受到合外力为

(2)小球离开电场时的速度为




碰撞过程中损失的机械能为
则:
解得: 
(3)由能量守恒得:
知识点
在静止的车厢内,用细绳a和b系住一个小球,绳a斜向上拉,绳b水平拉,如图所示。现让车从静止开始向右做匀加速运动,小球相对于车厢的位置不变,与小车静止时相比,绳a、b的拉力Fa、Fb变化情况是( )
正确答案
解析
略
知识点
如图所示,半径为R的环形塑料管竖直放置,AB直线跟该环的水平直径重合,且管的内径远小于环的半径。AB及其以下部分处于水平向左的匀强电场中,管的内壁光滑。现将一质量为m,带电量为+q的小球从管中A点由静止释放,小球受到的电场力跟重力相等,则以下说法中正确的是
正确答案
解析
略
知识点
如图所示,AB为半径为R=0.45m的光滑
(1)求小物体滑到轨道上的B点时对轨道的压力。
(2)求小物体刚滑到小车上时,小物体的加速度a1和小车的加速度a2各为多大?
(3)试通过计算说明小物体能否从小车上滑下?求出小车最终的速度大小。
正确答案
(1)FB=15N
(2)a1= 4m/s2;a2=2m/s2
(3)1.0m/s
解析
(1)小物体在圆弧上滑动,由动能定理得

圆弧最低点,由牛顿第二定律得
由牛顿第三定律得小物体对轨道的压力FB′=FB=15N
(2)小物体:
小车:
a1=4m/s2
a2=2m/s2
(3)设小物体没有从小车上滑下去,则最终两者速度相等



相对位移
物体没有从小车上滑下去,最终和小车以相同的速度运动

知识点
如图所示,小滑块A和B(可视为质点)套在固定的水平光滑杆上。一轻弹簧上端固定在P点,下端与滑块B相连接。现使滑块B静止在P点正下方的O点,O、P间的距离为h。某时刻,滑块A以初速度v0沿杆向右运动,与B碰撞后,粘在一起以O为中心位置做往复运动。光滑杆上的M点与O点间的距离为



求:
(1)滑块A与滑块B碰后瞬间共同速度v的大小;
(2)当滑块A、B运动到M点时,加速度a的大小;
(3)滑块A、B在往复运动过程中,最大速度vm的大小。
正确答案
见解析。
解析
(1)取A、B滑块为系统,由动量守恒定律有
所以
(2)当滑块运动到M点时,弹簧的长度
此时弹簧的弹力
根据牛顿第二定律
(3)当弹簧处于原长时,滑块的速度最大。取滑块A、B和弹簧为系统,由机械能守恒定律有
所以
知识点
真空中有两个带同种电荷的点电荷q1、q2,它们相距较近,固定q1,由静止释放q2,q2只在q1的库仑力作用下运动,则q2在运动过程中的速度( )
正确答案
解析
略
知识点
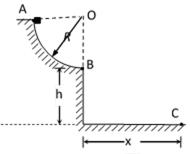
在竖直平面内有一个粗糙的
求:
(1)小滑块离开轨道时的速度大小;
(2)小滑块运动到轨道最低点时,对轨道的压力大小;
(3)小滑块在轨道上运动的过程中,克服摩擦力所做的功.
正确答案
见解析。
解析
(1)小滑块离开轨道后做平抛运动,设运动时间为t,初速度为v,则
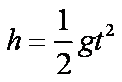
解得: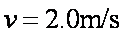
(2)小滑块到达轨道最低点时,受重力和轨道对它的弹力为N,根据牛顿第二定律: 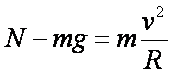
解得:
根据牛顿第三定律,轨道受到的压力大小
(3)在滑块从轨道的最高点到最低点的过程中,根据动能定理:
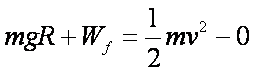
所以小滑块克服摩擦力做功为0.2J。
知识点
如图所示,在空中有一水平方向的匀强磁场区域,区域的上下边缘间距为h,磁感应强度为B。有一长度为L、宽度为b(b<h)、电阻为R、质量为m的矩形线圈紧贴磁场区域的上边缘从静止起竖直下落,当线圈的下边穿出磁场时,恰好以速率v匀速运动。已知重力加速度为g,求
(1)线圈匀速运动的速率v;
(2)穿过磁场区域过程中,线圈中产生的热量Q;
(3)线圈穿过磁场区域所经历的时间t。
正确答案
见解析
解析
(1)线圈匀速穿出磁场,产生的感应电动势为 
回路中的电流为 
此时线圈受到竖直向上的安培力 
由平衡条件得 
所以 
(2)线圈穿过磁场区域过程中,由功能关系 
所以 
(3)线圈进入磁场过程中,下边进入磁场时线圈的速率为0,上边进入磁场时线圈的速率为v1。当其速率为V时,由牛顿运动定律

又 
整理,得
求和,得
所以
故
接着线圈在磁场以g匀加速运动,有

最后线圈匀速穿出磁场,有

所以
知识点
16.如图所示,一根细线下端拴一个金属小球
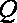

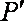
正确答案
解析
设细线与竖直方向的夹角为θ,细线的拉力大小为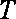
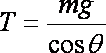
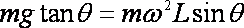
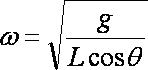
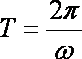
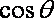
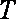
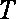
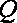
知识点
扫码查看完整答案与解析