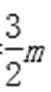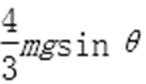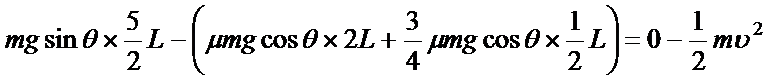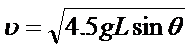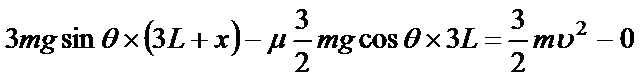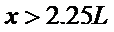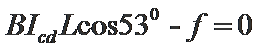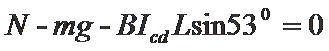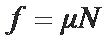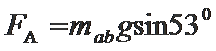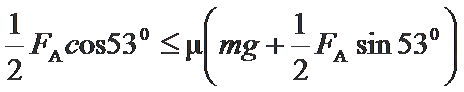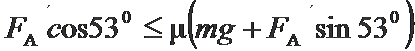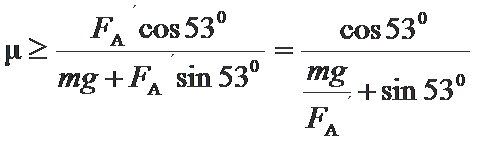- 牛顿运动定律
- 共1024题
14.如图,一质量为m的正方体物块置于风洞内的水平面上,一面与风速垂直,当风速为v0时刚好能推动该物块。已知风对物块的推力F∝Sv2,其中v为风速、S为物块迎风面积。当风速变为2v0时,刚好能推动用同一材料做成的另一正方体物块,则该物块的质量为( )
正确答案
解析
当风速为v0时刚好能推动该物块。已知风对物块的推力F∝Sv2,,由受力平衡得µmg=kSv2,,设该正方形的边长为a,则有µa3g=ka2v2,当风速变为2v0时,设带求正方形的边长为b,同理有µb3g=kb2(2v)2,解得b=4a,即待求正方体的边长是原来的4倍,体积是64倍,质量也是64倍
考查方向
解题思路
由平衡关系和正方体的体积计算质量关系
易错点
容易解得是4倍
知识点
19.滑雪运动中当滑雪板压在雪地时会把雪内的空气逼出来,在滑雪板与雪地间形成一个暂时的“气垫”,从而大大减小雪地对滑雪板的摩擦.然而当滑雪板相对雪地速度较小时,与雪地接触时间超过某一值就会陷下去,使得它们间的摩擦力增大.假设滑雪者的速度超过4 m/s时,滑雪板与雪地间的动摩擦因数就会由


(1)滑雪者从静止开始到动摩擦因数发生变化所经历的时间;
(2)滑雪者到达B处的速度;
(3)滑雪者在水平雪地上运动的最大距离。
正确答案
(1)
(2)
(3)
解析
(1)设滑雪者质量为m,滑雪者在斜坡上从静止至速度
由牛顿第二定律有:
解得:
故由静止开始到动摩擦因数发生变化所经历的时间:
(2)物体在斜面上改变动摩擦因数前
在斜面上改变动摩擦因数后
代入数据解得:
(3)设水平雪地上滑雪者速度由


由动能定理有:
所以滑雪者在水平雪地上运动的最大距离为:
考查方向
解题思路
对滑雪者在不同的过程中分别进行受力分析,列出牛顿定律公式及动能定理公式。
易错点
1、分析不同过程人受力;
2、列动能定理的公式
知识点
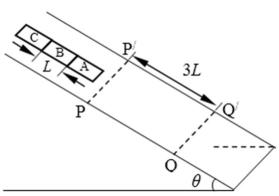
16.如图所示,倾角为θ的斜面上PP/、QQ/之间粗糙,且长为3L,其余部分都光滑.形状相同、质量分布均匀的三块薄木板A、B、C沿斜面排列在一起,但不粘接.每块薄木板长均为L,质量均为m,与斜面PP/、QQ/间的动摩擦因素均为2tanθ.将它们从PP/上方某处由静止释放,三块薄木板均能通过QQ/.重力加速度为g.求:
(1)薄木板A在PP/、QQ/间运动速度最大时的位置;
(2)薄木板A上端到达PP/时受到木板B弹力的大小;
(3)释放木板时,薄木板A下端离PP/距离满足的条件.
正确答案
(1)滑块A的下端离P处1.5L处时的速度最大
(2)F=
(3)释放时,A下端离PP/距离x>2.25L
解析
(1)将三块薄木板看成整体:当它们下滑到下滑力等于摩擦力时运动速度达最大值
μmxgcosθ=3mgsinθ
得到mx=
即滑块A的下端离P处1.5L处时的速度最大
(2)对三个薄木板整体用牛顿第二定律:3mgsinθ-μmgcosθ=3ma
得到 a=
对A薄木板用牛顿第二定律F+mgsinθ-μmgcosθ=ma
F=
(3)要使三个薄木板都能滑出QQ/处,薄木板C中点过QQ/处时它的速度应大于零。薄木板C全部越过PP/前,三木板是相互挤压着,全部在PP/、QQ/之间运动无相互作用力,离开QQ/时,三木板是相互分离的。
设C木板刚好全部越过PP/时速度为v
① 对木板C用动能定理:
②设开始下滑时,A的下端离PP/处距离为x,对三木板整体用动能定理:
得到x=2.25L
即释放时,A下端离PP/距离
考查方向
解题思路
见解析。
易错点
① 三块薄木板未粘连,速度不一致时会分离;
② 斜面上的物体若粗略的认为最大静摩擦力与滑动摩擦相等,则μ=tanθ是物体能否沿斜面下滑的临界条件;
③ 研究对象和研究过程的选取不当,导致求解困难。
知识点
16.如图,水平传送带始终保持着大小为V1=2m/s的速度水平向右运动,一质量为m=1kg的物体以V2=4m/s的速度沿传送带水平向左由B向A处运动,已知物体与传送带间的摩擦因数μ=0.2,A、B两点间距离S=6m,从木块放上传送带的B点开始到木块离开传送带为止,(g=10m/s2)试求:
(1)物体在传送带上运动的时间?(2)传送带对物块做功为多大?
正确答案
(1)物体在传送带上运动的时间为4.5s.(2)传送带对物块做功为-6J
解析
(1)物体相对地向左运动的过程,根据牛顿第二定律得:
加速度大小为 a=μmg /m=μg=0.2×10=2m/s2,
设经过时间t1速度减为零,则由0=v2-at1得 t1= v2 /a=4/2s=2s,这段时间内的位移x1=v2/2 t1=4/2×2m=4m;
再设物体向右运动经过时间t2速度与传送带相等,则v1=at2,得t2= v1/a=2/2s=1s这段时间内的位移x2=
(2)向左运动过程,根据动能定理得:传送带对物块做功为W1=0-

考查方向
本题主要考查牛顿第二定律;匀变速直线运动的位移与时间的关系;功的计算
解题思路
(1)物体先向左做匀减速运动,速度减为零后向右做匀加速运动,速度与传送带速度相等后匀速,根据运动学公式,可求出运动的总时间.(2)根据动能定理求解传送带对物块做功.
易错点
对于传送带问题,通常运动分两个过程,要对这两个过程分别进行运动分析和受力分析,然后结合牛顿第二定律和运动学公式求解
知识点
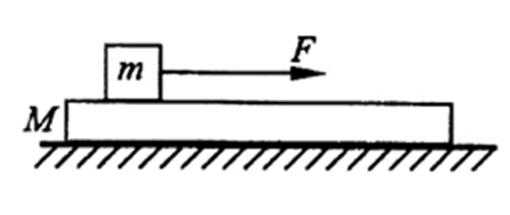
14.如图所示,质量为m的木块在质量为M的长木板上受到水平向右的拉力F的作用下向右滑行,长木板处于静止状态.已知木块与木板间的动摩擦因数为μ1,木板与地面间的动摩擦因数为μ2.下列说法正确的是( )
正确答案
解析
A、对M分析,在水平方向受到m对M的摩擦力和地面对M的摩擦力,两个力平衡,则地面对木板的摩擦力f=μ1mg.故A正确,B错误.C、无论F大小如何,m在M上滑动时对M的摩擦力大小不变,M在水平方向上仍然受到两个摩擦力处于平衡,不可能运动.故C错误,D正确
考查方向
本题主要考查牛顿第二定律;摩擦力的判断与计算
解题思路
隔离对M分析,抓住木板处于静止状态,根据共点力平衡求出地面对木板的摩擦力大小.无论改变F的大小,只要m在木板上滑动,则m对M的摩擦力大小不变,木板仍然保持静止
易错点
本题中木板受到地面的摩擦力是静摩擦力,不能根据滑动摩擦力公式求解,f2=μ2(m+M)g是错误的
知识点
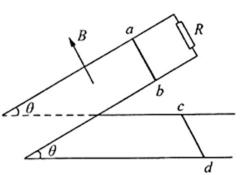
21.如图所示,电阻不计的“∠”型足够长且平行的导轨,间距L=1 m,导轨倾斜部分的倾角
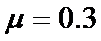
(1)ab棒由静止释放,当滑至某一位置时,cd棒恰好开始滑动。求这一时刻ab棒中的电流;
(2)若ab棒无论从多高的位置释放,cd棒都不动,分析ab棒质量应满足的条件;
(3)若cd棒与导轨间的动摩擦因数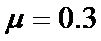
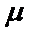
正确答案
(1)Iab=2Icd=3.34A
(2)ma
(3)当ab棒质量无限大,在无限长轨道上最终一定匀速运动,安培力FA趋于无穷大,cd棒所受安培力FAˊ亦趋于无穷大,有:μ≥=0.75
解析
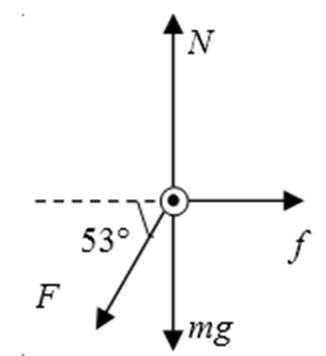
(1)cd棒刚要开始滑动时,其受力分析如图所示。
由平衡条件得:
又因为
联立以上三式,得Icd=1.67A,
所以Iab=2Icd=3.34A
(2)ab棒在足够长的轨道下滑时,最大安培力
cd棒所受最大安培力应为
由以上两式联立解得:ma
(3)ab棒下滑时,cd棒始终静止,有:
解得:
当ab棒质量无限大,在无限长轨道上最终一定匀速运动,安培力FA趋于无穷大,cd棒所受安培力FAˊ亦趋于无穷大,有:μ≥=0.75
考查方向
解题思路
1、 由右手定则求出电流方向,再由左手定则求出安培力方向。
2、画出等效电路
易错点
感应电流方向的判断, 安培力方向的判断。
知识点
8.如图所示,光滑绝缘的水平面内存在场强为E的匀强电场,长度为L绝缘光滑的挡板AC与电场方向夹角为30°.现有质量相等、电荷量均为Q的甲、乙两个带电体从A处出发,甲由静止释放,沿AC边无摩擦滑动,乙垂直于电场方向以一定的初速度运动,甲、乙两个带电体都通过C处.则甲、乙两个带电体( )
正确答案
解析
由于甲、乙初始位置和终了位置均一致,故位移相同,A选项正确;
对于甲和乙两带电体分别写出动能定理:WG+QUAC=ΔEk甲;WG+QUAC=ΔEk乙,尽管合外力做功相同,但甲、乙初动能不同,所以到达C点的末动能不同,又其质量相同,所以到达C点的速度不相等,B选项错误;对于两带电体,电场力对它们所做的功是一致的,均为W=EQ(

考查方向
解题思路
本题关键在于甲、乙两带电体运动到C时的时间和电场力做功问题,先分别对两物体受力分析,再根据功的定义即可解决问题。
易错点
位移是初位置指向末位置的有向线段;电场力做功等于电势能的减小量而非变化量。
知识点
3. 一质量为m的木块静止在光滑的水平面上,从t=0开始,将一个大小为F的水平恒力作用在该木块上,在t=t1时刻力F的瞬时功率是( )
正确答案
解析
由牛顿第二定律可以得到,F=ma,所以


考查方向
功率、平均功率和瞬时功率
解题思路
物体做匀加速直线运动,根据牛顿第二定律可以求得物体的加速度的大小,再由速度公式可以求得物体的速度的大小,由P=FV来求得瞬时功率.
易错点
关键求出t1时刻物体的速度,根据瞬时功率表达式列式.
教师点评
本题考查了功率、平均功率和瞬时功率,在近几年的各省高考题出现的频率较高,常与功的计算、动能定理等知识点交汇命题.
知识点
激流勇进是游乐园常有的机动游乐项目。其工作原理是由主动轮将游船沿较长的倾斜轨道提升至一定高度,然后船只从高处滑下,冲入水中,溅起很高且美丽的水花,整个过程刺激又有趣。其工作过程可以简化为如下情景:如图所示,左侧倾角α=30°的轨道AB(其长L1= 30 m)上相互间隔安装着主动轮,主动轮与游船间的动摩擦因数u1=
12.游船从轨道左侧运动到右侧底端(船头刚好触及水面)所用总时间;
13.动力装置在游船达到恒定速率前后(没有到达BC轨道)需增加的功率之比。
正确答案
19.3s
解析
游船加速上升阶段,设其加速度为a1,有牛顿第二定律有:
μ1mgcos30°-mgsin30°=ma1
代入数据解得:a1=2.5m/s2
从静止达到共同速度所用时间为t1,上移的距离为x1,有速度时间公式可得:v=a1t1
主动轮的线速度为:v=ωr=0.2×10m/s=2m/s
联立并代入数据解得:t1=0.8s
匀速运动的位移为:x2=L1+L3-x1=(30+3-0.8)m=32.2m
匀速运动的时间为:
游船在右侧轨道上运价速运动,加速度为a2,由牛顿第二定律有:
mgsinβ-μ2mgcosβ=ma2
代入数据解得:
加速运动的时间为t3,游船在右侧轨道上发生的位移为:
联立并代入数据解得:t3=2.4s
所需总时间为:t=t1+t2+t3=19.3s
考查方向
牛顿第二定律
解题思路
由牛顿第二定律求得左侧轨道和右侧轨道的加速度,利用运动学公式求得时间.
易错点
关键抓住运动过程的分析,分段求出时间.
正确答案
解析
游船达到恒定速率前动力装置增加的功率为:
P1=f1v=(μ1mgcosα)v
游船达到恒定速率后动力装置增加的功率为:
P2=f2v=(mgsinα)v
动力装置在游船达到恒定速率前后(没有到达BC轨道)需增加的功率之比:
考查方向
功率、平均功率和瞬时功率
解题思路
根据P=fv求得动力装置在游船达到恒定速率前后(没有到达BC轨道)需增加的功率.
易错点
关键根据P=FV列出游船达到恒定速率前动力装置增加的功率与游船达到恒定速率后动力装置增加的功率的表达式.
激流勇进是游乐园常有的机动游乐项目。其工
作原理是由主动轮将游船沿较长的倾斜轨道提升至一
定高度,然后船只从高处滑下,冲入水中,溅起很高且美
丽的水花,整个过程刺激又有趣。其工作过程可以简化
为如下情景:如图9所示,左侧倾角α=30°的轨道AB
(其长L1= 30 m)上相互间隔安装着主动轮,主动轮与游
船间的动摩擦因数u1=
导向轮(不会提供动力),导向轮与游船间的动摩擦因数均为u2=41/72;左右两侧轨道通过一段
平滑轨道BC(其长L3=3 m)相连,两相邻主动轮(或导向轮)间的距离s0 =1 m。长为L0=
2 m的游船上坐着两个游客,总质量为180 kg,从左侧轨道如图所示的位置由静止开始被主
动轮带动向上运动(主动轮的半径r=0.2 m,恒定的角速度ω=10 rad/s),达恒定的速率后,
一直以此速率运动到游船尾部刚好与右侧轨道的上端C点平齐的位置,之后在导向轮上向
下滑动。已知g=10 m/s2,sin 53°=0.8,cos53°=0.6。求
2 m的游船上坐着两个游客,总质量为180 kg,从左侧轨道如图所示的位置由静止开始被主
动轮带动向上运动(主动轮的半径r=0.2 m,恒定的角速度ω=10 rad/s),达恒定的速率后,
一直以此速率运动到游船尾部刚好与右侧轨道的上端C点平齐的位置,之后在导向轮上向
下滑动。已知g=10 m/s2,sin 53°=0.8,cos53°=0.6。求
16.游船从轨道左侧运动到右侧底端(船头刚好触及水面)所用总时间;
17.动力装置在游船达到恒定速率前后(没有到达BC轨道)需增加的功率之比。
正确答案
19.3s
解析
游船加速上升阶段,设其加速度为a1,有牛顿第二定律有:
μ1mgcos30°-mgsin30°=ma1
代入数据解得:a1=2.5m/s2
从静止达到共同速度所用时间为t1,上移的距离为x1,有速度时间公式可得:v=a1t1
主动轮的线速度为:v=ωr=0.2×10m/s=2m/s
联立并代入数据解得:t1=0.8s
匀速运动的位移为:x2=L1+L3-x1=(30+3-0.8)m=32.2m
匀速运动的时间为:
游船在右侧轨道上加速运动,加速度为a2,由牛顿第二定律有:mgsinβ-μ2mgcosβ=ma2
代入数据解得:
加速运动的时间为t3,游船在右侧轨道上发生的位移为:
联立并代入数据解得:t3=2.4s
所需总时间为:t=t1+t2+t3=19.3s
考查方向
牛顿第二定律;匀变速直线运动规律的综合运用
解题思路
由牛顿第二定律求得上升阶段加速度和下降阶段的加速度,利用运动学公式求得时间 .
易错点
关键分清物理过程,正确的受力分析求出两个阶段的加速度.
正确答案
3:2
解析
游船达到恒定速率前动力装置增加的功率为:
P1=f1v=(μ1mgcosα)v
游船达到恒定速率后动力装置增加的功率为:
P2=f2v=(mgsinα)v
动力装置在游船达到恒定速率前后(没有到达BC轨道)需增加的功率之比:
考查方向
功率、平均功率和瞬时功率
解题思路
根据P=fv求得动力装置在游船达到恒定速率前后(没有到达BC轨道)需增加的功率.
易错点
关键由功率表达式求出增加的功率.
扫码查看完整答案与解析