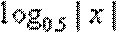- 圆锥曲线与方程
- 共2033题
设向量a=(

(1)若|a|=|b|,求x的值;
(2)设函数f(x)=a·b,求f(x)的最大值。
正确答案
(1)
(2)
解析
(1)由|a|2=
|b|2=cos2x+sin2x=1,
及|a|=|b|,得4sin2x=1.
又x∈

所以
(2)f(x)=a·b=

当

所以f(x)的最大值为
知识点
设

正确答案
解析
略
知识点
在复平面内,复数
正确答案
解析
略
知识点
已知双曲线的方程为


正确答案

解析
略
知识点
已知曲线


(1)讨论曲线
(2)若






正确答案
见解析
解析
(1)当


当



当


当


当


(2)由

因为



设












知识点
如图所示,已知双曲线的中心在坐标原点O,焦点分别是F1(-2,0)F2(2,0),且双曲线经过点P(2,3)。
(1) 求双曲线的标准方程;
(2)设点A是双曲线的右顶点,若直线l平行于直线AP,且l与双曲线交于M,N两点,若
︱+︱=4,试求直线l的方程
正确答案
见解析
解析
(1)由题意得:双曲线焦点在x轴上,且c=2
由双曲线定义得:
=2
∴
∴双曲线的标准方程为
(2)根据双曲线的标准方程得:点A的坐标为(1,0)
∴直线AP的斜率为
∵直线l平行于直线AP
∴设直线l的方程为
联立方程

所以 
因为直线 l 与双曲线有两个交点,
所以 (6 b)2-4×6×(b 2+3)>0,
解得 b<- 或 b>,即 b 的取值范围是 { b | b<- 或 b>}。
∴

所以,所求的直线方程为:
知识点
飞船返回仓顺利到达地球后,为了及时将航天员救出,地面指挥中心在返回仓预计到达区域安排三个救援中心(记为A,B,C),B在A的正东方向,相距6km,C在B的北偏东30°,相距4km,P为航天员着陆点,某一时刻A接到P的求救信号,由于B、C两地比A距P远,因此4s后,B、C两个救援中心才同时接收到这一信号,已知该信号的传播速度为1km/s。
(1)求A、C两个救援中心的距离;
(2)求在A处发现P的方向角;
正确答案
见解析。
解析
(1)
以AB中点为坐标原点,AB所在直线为x轴建立平面直角坐标系,则
则
即A、C两个救援中心的距离为
(2)
又
∴双曲线方程为
BC的垂直平分线的方程为
联立两方程解得:
∴∠PAB=120°
所以P点在A点的北偏西30°处
知识点
已知双曲线与椭圆
正确答案
解析
略
知识点
已知

正确答案
解析
略
知识点
已知双曲线C的两个焦点坐标分别为

(1)求双曲线C的标准方程;
(2)经过点M(2,1)作直线l交双曲线C的右支于A,B两点,且M为AB的中点,求直线l的方程.
(3)已知定点G(1,2),点D是双曲线C右支上的动点,求
正确答案
见解析。
解析
(1)依题意,得双曲线C的实半轴长为a=1,焦半距为c=2,
所以其虚半轴长
又其焦点在x轴上,所以双曲线C的标准方程为
(2)设A、B的坐标分别为

两式相减,得
因为M(2,1)为AB的中点,所以
所以

故AB所在直线l的方程为

(3)由已知,得

所以

因为
所以
故

知识点
已知椭圆C:



(1)求椭圆C的方程;
(2)已知圆M:

正确答案
见解析。
解析
(1)因为椭圆C的离心率


因为抛物线

所以



(2)(i)当直线
因为直线

由


则以AB为直径的圆的方程为
(ii)当直线
因为直线

由


则以AB为直径的圆的方程为
显然以上两圆都经过点O(0,0),(8分)
(iii)当直线
设直线

由


所以设



所以
所以
因为直线


整理,得
将②代入①,得
综上可知,以AB为直径的圆过定点(0,0),(13分)
知识点
对于双曲线




(1)当






(2)若双曲线









(3)若双曲线






正确答案
(1)

解析
解析:(1)∵

由

可得 
∴

(2)双曲线





解得
当



由


∵


∴
∴
由对称性知,当

(3)设



∴直线

直线

由①②得
∵ 

∴

知识点
5.下列函数中,既是偶函数,又在区间(0,3)内是增函数的是
正确答案
解析



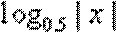
知识点
已知双曲线


正确答案
解析
由题意可得由题意得A(0,b),C(0,﹣b),B(﹣a,0),F(﹣c,0),
∴







知识点
1. 复数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析