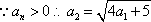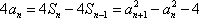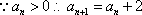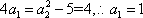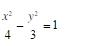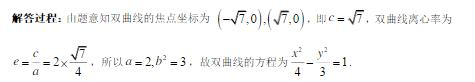- 圆锥曲线与方程
- 共2033题
已知数列{an}的前n项和Sn＝kcn－k(其中c，k为常数)，且a2＝4，a6＝8a3.
(1)求an；
(2)求数列{nan}的前n项和Tn.
正确答案
(1) an＝2n. ;(2) (n－1)2n＋1＋2.
解析
(1)由Sn＝kcn－k，
得an＝Sn－Sn－1＝kcn－kcn－1(n≥2)，
由a2＝4，a6＝8a3，得kc(c－1)＝4，kc5(c－1)＝8kc2(c－1)，
解得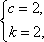
于是an＝2n.
(2)
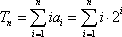
Tn＝2＋2·22＋3·23＋4·24＋…＋n·2n，
Tn＝2Tn－Tn＝－2－22－23－24－…－2n＋n·2n＋1＝－2n＋1＋2＋n·2n＋1＝(n－1)2n＋1＋2.
知识点
设各项均为正数的数列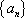
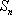
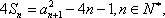
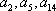
（1）证明：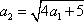
（2）求数列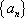
（3）证明：对一切正整数
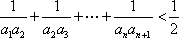
正确答案
见解析
解析
（1）当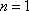
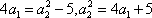
（2）当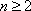
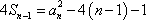
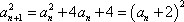
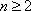
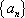
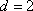
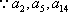
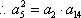
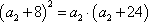
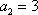
由（1）可知，
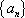
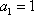
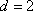
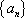
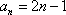
（3）
知识点
已知双曲线
正确答案
2
解析
由
知识点
已知双曲线C1：
正确答案
1;2
解析
∵C1与C2的渐近线相同，∴
又C1的右焦点为F(
∴a2＝1，b2＝4，∴a＝1，b＝2
知识点
已知三点O(0,0)，A(－2,1)，B(2,1)，曲线C上任意一点M(x，y)满足
(1)求曲线C的方程；
(2)点Q(x0，y0)(－2＜x0＜2)是曲线C上的动点，曲线C在点Q处的切线为l，点P的坐标是(0，－1)，l与PA，PB分别交于点D，E，求△QAB与△PDE的面积之比。
正确答案
(1) x2＝4y； (2)2
解析
(1)由
得
由已知得
化简得曲线C的方程：x2＝4y.
(2)直线PA，PB的方程分别是y＝－x－1，y＝x－1，曲线C在Q处的切线l的方程是
分别联立方程组
则xE－xD＝2，|FP|＝1－
故S△PDE＝
则
知识点
若双曲线
正确答案
48
解析
根据双曲线方程：
知识点
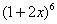
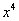
正确答案
240
解析
由二项式定里，展开式单项为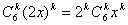
代入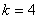
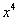
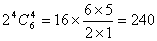
知识点
已知双曲线
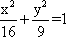
正确答案
解析
知识点
已知双曲线
A
B
C
D
正确答案
解析
双曲线
又∵
∴
知识点
若
A
B
C
D
正确答案
解析
知识点
双曲线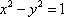
A
B
C1
D
正确答案
解析
本题考查的是双曲线的性质，因为双曲线的两个顶点到两条渐近线的距离都相等，故可取双曲线的一个顶点为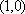
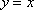
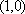
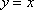
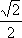
知识点
设直线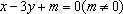
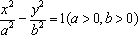
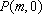
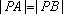
正确答案
解析
由双曲线的方程数知，其渐近线方程为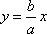
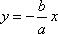
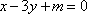
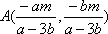
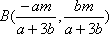
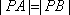
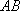
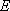
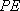
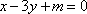
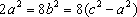
知识点
设O为坐标原点，
Ax±
B
Cx±
D
正确答案
解析
选D，本题将解析几何与三角知识相结合，主要考察了双曲线的定义、标准方程，几何图形、几何性质、渐近线方程，以及斜三角形的解法，属中档题
知识点
设圆锥曲线I的两个焦点分别为F1，F2，若曲线I上存在点P满足
A
B
C
D
正确答案
解析
当曲线为椭圆时
当曲线为双曲线时
知识点
已知双曲线x2－y2＝1，点F1，F2为其两个焦点，点P为双曲线上一点，若PF1⊥PF2，则|PF1|＋|PF2|的值为__________。
正确答案
解析
设|PF1|＝m，|PF2|＝n，根据双曲线的定义及已知条件可得|m－n|＝2a＝2，m2＋n2＝4c2＝8，
故mn＝2，(|PF1|＋|PF2|)2＝(m＋n)2＝(m－n)2＋4mn＝4＋4×2＝12，于是|PF1|＋|PF2|＝
知识点
扫码查看完整答案与解析