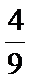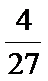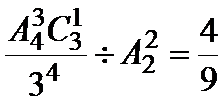- 古典概型的概率
- 共151题
16.甲、乙、丙、丁四人排成一排,其中甲、乙两人相邻的概率是
正确答案
解析
由A44=24,A22*A33=12,则P=
考查方向
本题主要考查排列组合、概率计算
解题思路
1、求出4人排队的总方法数;
2、求出甲乙相邻的方法数,即可得到结果。
A选项不正确,B选项不正确,D选项不正确,所以选C选项。
易错点
本题易在求方法数时发生错误。
知识点
12.正四面体的四个面上分别写有数字0,1,2,3把两个这样的四面体抛在桌面上,则露在外面的6个数字之和恰好是9的概率为___________.
正确答案
解析
由题意,试验发生所包含的事件是2个均匀的正四面体与桌面接触,共有4×4=16种情况.一个正四面体的四个面的数字和为6,则露在外面的6个数字之和恰好是9即与桌面接触两个面的数字和为3,它包括0+3、1+2、2+1、3+0四种情况.∴所求概率为
考查方向
本题考查等可能事件的概率计算,是容易题,在近几年各地高考中频频出现.
解题思路
先求试验所包含的事件的所有种数,然后寻找符合要求的试验种数,即可得到概率.
易错点
解题的关键是正确运用列举法,分析得到基本事件的个数.
知识点
7.袋中有形状、大小都相同的4只球,其中1只白球,1只红球,2只黄球,从中一次随机摸出2只球,则这2只球中有黄球的概率为___________
正确答案
解析
考查方向
解题思路
本题考查运用乘法原理求这2只球中没有黄球的概率,再利用互斥事件的性质求解。解题步骤如下:
易错点
本题必须注意审题,忽视则会出现错误。
知识点
9.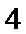

正确答案
解析
首先计算总数,4个人,每个人都可以在3项不同的活动中任选一项,也就是每个人都有3中选择,所以总数是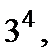
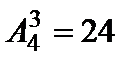
考查方向
解题思路
首先根据邮筒原理,算出总数,然后来计算每一项至少有一人参加共有多少种,最后计算概率
易错点
1、总数是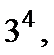
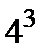
2、不会计算每项至少有一人参加的数量
知识点
18. 现有甲、乙两个靶,某射手向甲靶射击一次,命中的概率为

(Ⅰ)求该射手恰好命中一次的概率;
(Ⅱ)求该射手的总得分

正确答案
见解析
解析
(Ⅰ)记“该射手恰好命中一次”为事件



由题意知,

由于
(Ⅱ)根据题意,

根据事件的独立性和互斥性得



故
所以
考查方向
解题思路
第一问将所有可能的情况列举出求解,第二问根据随机变量分布列的概念及特征,一次写出当随机变量取不同值得情况
易错点
列举情况不全面
知识点
扫码查看完整答案与解析