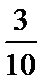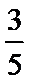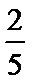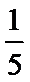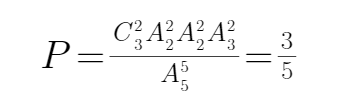- 古典概型的概率
- 共151题
7.袋中有形状、大小都相同的4只球,其中1只白球,1只红球,2只黄球,从中一次随机摸出2只球,则这2只球中有黄球的概率为___________
正确答案
解析
考查方向
解题思路
本题考查运用乘法原理求这2只球中没有黄球的概率,再利用互斥事件的性质求解。解题步骤如下:
易错点
本题必须注意审题,忽视则会出现错误。
知识点
11.某校组织由5名学生参加的演讲比赛,采用抽签法决定演讲顺序,在“学生



正确答案
解析
解:方法一:“学生A和B都不是第一个出场,B不是最后一个出场”的出场顺序为:分为两类.
第一类:A最后一个出场,从除了B之外的3人选1人安排第一个,其它的任意排,故有A31A33=18种,
第二类:A不是最后一个出场,从除了A,B之外的3人选2人安排在,第一个或最后一个,其余3人任意排,故有A32A33=36种,
故学生A和B都不是第一个出场,B不是最后一个出场的种数18+36=54种,
“学生A和B都不是第一个出场,B不是最后一个出场”的前提下,学生C第一个出场的”的出场顺序为:分为两类
第一类:学生C第一个出场,A最后一个出场,故有A33=6种,
第二类:学生C第一个出场,A不是最后一个出场,从除了A,B之外的2人选1人安排在最后一个,其余3人任意排,故有A21A33=12种,
故在“学生A和B都不是第一个出场,B不是最后一个出场”的前提下,学生C第一个出场的种数6+12=18种,
故学生C第一个出场的概率为
方法二:先排B,有A31(非第一与最后),再排A有A31(非第一)种方法,其余三个自由排,共有A31A31A33=54这是总结果;
学生C第一个出场,先排B,有A31(非第一与最后),再排A有A31,C第一个出场,剩余2人自由排,故有A31A31A22=18种,
故学生C第一个出场的概率为
故选:A.
考查方向
解题思路
方法一:由题意,“学生A和B都不是第一个出场,B不是最后一个出场”的出场顺序为:分为两类,求取种数,再满足其前提下,学生C第一个出场顺序也为两类,再根据概率公式计算即可,
方法二:直接根据分步计数原理,可得,再根据概率公式计算即可.
易错点
不重不漏是关键,容易出现次序问题。
知识点
8.袋中装有偶数个球,其中红球、黑球各占一半.甲、乙、丙是三个空盒.每次从袋中任意取出两个球,将其中一个球放入甲盒,如果这个球是红球,就将另一个球放入乙盒,否则就放入丙盒.重复上述过程,直到袋中所有球都被放入盒中,则()
正确答案
解析
解:取两个球共有4种情况:
①红+红,则乙盒中红球数加1个;
②黑+黑,则丙盒中黑球数加1个;
③红+黑(红球放入甲盒中),则乙盒中黑球数加1个;
④黑+红(黑球放入甲盒中),则丙盒中红球数加1个.
设一共有球2a个,则a个红球,a个黑球,甲中球的总个数为a,其中红球x个,黑球y个,x+y=a.
则乙中有x个球,其中k个红球,j个黑球,k+j=x;
丙中有y个球,其中l个红球,i个黑球,i+l=y;
黑球总数a=y+i+j,又x+y=a,故x=i+j
由于x=k+j,所以可得i=k,即乙中的红球等于丙中的黑球.
故选B.
考查方向
该题考查了推理与证明,重点是找到切入点逐步进行分析,对学生的逻辑思维能力有一定要求,中档题
解题思路
分析理解题意:乙中放红球,则甲中也肯定是放红球;往丙中放球的前提是放入甲中的不是红球,据此可以从乙中的红球个数为切入点进行分析.
易错点
列举计数的关键是要有规律,从而确保不重不漏.另外注意对立事件概率公式的应用
知识点
某校课改实行选修走班制,现有甲,乙,丙,丁四位学生准备选修物理,化学,生物三个科目.每位学生只选修一个科目,且选修其中任何一个科目是等可能的.
21.恰有2人选修物理的概率;
22.选修科目个数
正确答案
详见解析
解析
所有可能的选修方式有34种,恰有2人选修物理的方式
考查方向
随机事件发生的概率
解题思路
先求出所有可能的情况,然后求出恰有2人选修物理的情况,二者的比例为发生的概率
易错点
考虑问题不全面,有重或有漏
正确答案
详见解析
解析
ξ的所有可能值为1,2,3.又
综上知,ξ有分布列
ξ 1 2 3
从而有
考查方向
随机变量的分布列,随机变量的数学期望
解题思路
先求出随机变量的所有情况,然后分别算出对应的概率,进而求出分布列和数学期望
易错点
计算错误。分布列考虑情况不全面
教师点评
求随机变量分布列时,要注意书写步骤,计算也要准确
某校课改实行选修走班制,现有甲,乙,丙,丁四位学生准备选修物理,化学,生物三个科目.每位学生只选修一个科目,且选修其中任何一个科目是等可能的.
21.恰有2人选修物理的概率;
22.选修科目个数
正确答案
恰有2人选修物理的概率为
解析
所有可能的选修方式有34种,恰有2人选修物理的方式
考查方向
这是等可能性事件的概率计算问题.
解题思路
利用排列组合相关知识,结合题意,求出概率。
易错点
考虑情况不全面,可能的情况算错
教师点评
要对排列组合和概率知识掌握全面
正确答案
详见解析
解析
ξ的所有可能值为1,2,3.又
综上知,ξ有分布列
ξ 1 2 3
P
从而有
考查方向
求随机变量的分布列和期望
解题思路
先求出随机变量的所有可能性以及对应的概率,然后求其分布列和期望
易错点
求分布列时错误,考虑情况不全面
教师点评
求分布列的时候,要注意解题步骤,和书写格式
8.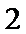
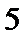
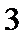
正确答案
解析
根据题意可知,
所以选B
考查方向
排列和组合的应用 随机事件发生的概率
解题思路
先算出所有可能的情况,然后算出发生的概率
易错点
考虑情况不全面
知识点
某小学对五年级的学生进行体质测试.已知五年级一班共有学生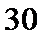
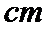
男生成绩在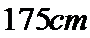
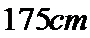
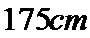
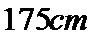
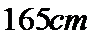
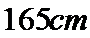
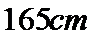
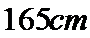
19.在五年级一班的男生中任意选取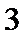
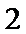
20.若从五年级一班成绩“合格”的学生中选取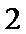

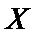
正确答案
详见解析
解析
解:(Ⅰ)设 “仅有两人的成绩合格”为事件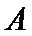
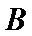
至少有两人的成绩是合格的概率为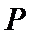
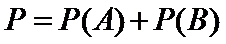
其中有8人合格,从而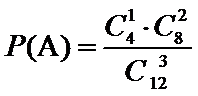

所以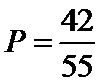
考查方向
概率与统计
解题思路
先求出仅有两人成绩合格的概率,再求出有三人成绩合格的概率,然后求出至少有两人成绩合格的概率
教师点评
正确分析“至少”“至多”等概念所表达的意思
正确答案
详见解析
解析
(Ⅱ)因为女生共有18人,其中有10人合格,依题意,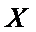
则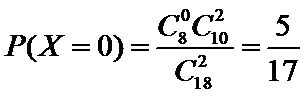
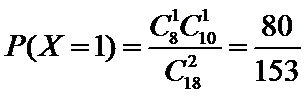
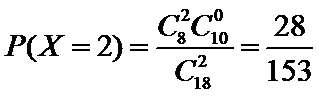
因此,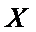
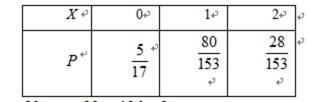
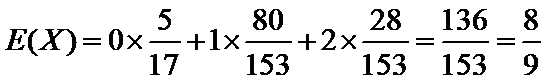
(或是,因为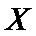
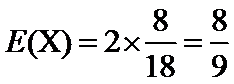
考查方向
随机变量的分布列,随机变量的数字特征
解题思路
先确定随机变量可能取的值,然后计算其分布列和数学期望
教师点评
列分布列时要注意,不要计算失误
某市在以对学生的综合素质评价中,将其测评结果分为“优秀、合格、不合格”三个等级,其中不小于80分为“优秀”,小于60分为“不合格”,其它为“合格”.
19.某校高一年级有男生500人,女生4000人,为了解性别对该综合素质评价结果的影响,采用分层抽样的方法从高一学生中抽取了45名学生的综合素质评价结果,其各个等级的频数统计如下表:
根据表中统计的数据填写下面

20.以(1)中抽取的45名学生的综合素质评价等级的频率作为全市各个评价等级发生的概率,且每名学生是否“优秀”相互独立,现从该市高一学生中随机抽取3人.
(i)求所选3人中恰有2人综合素质评价为“优秀”的概率;
(ii)记

参考公式:

临界值表:
正确答案
详见解析
解析
(1)设从高一年级男生中抽出

∴
而
∴没有
考查方向
概率与统计,分层抽样
解题思路
求解计算K值的参数的值,进而求出K值,利用K值判断
易错点
计算K值错误
教师点评
要熟练掌握求K值的各项参数所表达的意思是什么
正确答案
详见解析
解析
(2)(i)由(1)知等级为“优秀”的学生的频率为

记“所选3名学和g中恰有2人综合素质评价‘优秀’学生”为事件


(ii)由题意知,随机变量
∴随机变量

考查方向
随机变量的分布列,随机变量的数学期望
解题思路
求出随机变量各项取值的概率,然后计算数学期望
教师点评
随机变量
7.若两名教师与四名同学排成一列,求只有一名学生排在两名教师之间的概率( )
正确答案
解析
有




考查方向
本题主要考察了排列组合,古典概型,排列中捆绑法和插空法的应用
解题思路
先在4名学生中取出1人,将其放进2名教师中间,教师与学生捆绑将其3人看成一个元素,与其他三人进行全排列
易错点
本题易忽略两教师之间的顺序
知识点
国家旅游局确定2016年以“丝绸之路旅游年”为年度旅游宣传主题,甘肃武威为配合国家旅游局,在每张门票后印有不同的“丝绸之路徽章”。某人利用五一假期,在该地游览了文庙,白塔寺,沙漠公园,森林公园,天梯山石窟五处景点,并收集文庙纪念徽章3枚,白塔纪念徽章2枚,其余三处各1枚.,现从中任取4枚.
17.求抽取的4枚中恰有3个景点的概率;
18.抽取的4枚徽章中恰有文庙纪念徽章的个数为

正确答案
详见解析
解析
记“抽取的4枚徽章中恰有3个景点”为事件A ……………1分

考查方向
离散型随机变量的期望与方差;古典概型及其概率计算公式;离散型随机变量及其分布列
解题思路
记“抽取的4枚徽章中恰有3个景点”为事件A,由此利用互斥事件概率加法公式能求出抽取的4枚中恰有3个景点的概率.
易错点
求概率时错误
正确答案
详见解析
解析







.
……………12分

考查方向
离散型随机变量的期望与方差;古典概型及其概率计算公式;离散型随机变量及其分布列
解题思路
ξ的可能取值为0,1,2,3,分别求出相应的概率,由此能求出ξ的分布列及数学期望.
易错点
求分布列时有重复或遗漏
扫码查看完整答案与解析