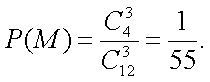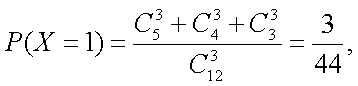古典概型的概率
共151题

· 古典概型的概率

古典概型的概率
共151题

热门试卷

X 查看更多试卷

题型：简答题

简答题 · 12 分

己知A、B两盒中都有红球、白球，且球的形状、大小都相同，盒子A中有m个红球与10-m个白球，盒子B中有10-m个红球与m个白球(0<m<10).

（1）分别从A、B中各取一个球，ξ表示红球的个数；

①请写出随机变量ξ的分布列，并证明E(ξ)等于定值；

②当m为何时， D(ξ)取到最小值，并求出最小值。

（2）在盒子A中不放回地摸取3个球，事件E：在第一次取到红球后，以后两次都取到白球，事件F：在第一次取到白球后，以后两次都取到红球，若概率P(E)=P(F)，求m的值。

正确答案

见解析

解析

（1）分布列为：

为定值。………5′

，

∵1≤m≤9(m∈N*)，∴当m=1或m=9，时，D(ξ)最小，最小值为.………8′

（2），

∵P(E)=P(F)，∴，∴m=5.………12′

知识点

古典概型的概率

题型：简答题

简答题 · 10 分

某品牌汽车4店经销，，三种排量的汽车，其中，，三种排量的汽车依次有5，4，3款不同车型，某单位计划购买3辆不同车型的汽车，且购买每款车型等可能。

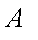
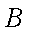
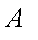
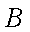
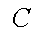
（1）求该单位购买的3辆汽车均为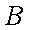种排量汽车的概率；

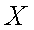
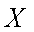
（2）记该单位购买的3辆汽车的排量种数为，求的分布列及数学期望。

正确答案

见解析。

解析

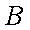
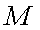
（1）设该单位购买的3辆汽车均为种排量汽车为事件，则

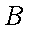
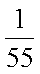
所以该单位购买的3辆汽车均为种排量汽车的概率为，

（2）随机变量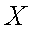的所有可能取值为1，2，3.

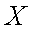
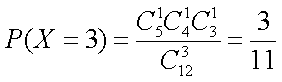
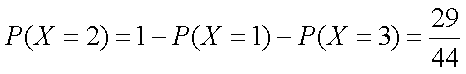
所以的分布列为

，

。

所以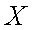的概率分布为

数学期望。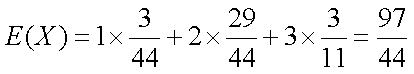

知识点

古典概型的概率离散型随机变量及其分布列、均值与方差

题型：单选题

单选题 · 5 分

甲、乙两人玩猜数字游戏，先由甲心中想一个数字，记为，再由乙猜甲刚才所想的数字，把乙猜的数字记为，其中，若，就称甲乙“心有灵犀”. 现任意找两人玩这个游戏，则他们“心有灵犀”的概率为（）

正确答案

解析

任意找两人玩这个游戏，共有中猜字结果，其中满足的有如下情形：

①若，则；② 若，则；③ 若，则；④ 若，则；⑤ 若，则；⑥ 若，则，总共16种，故他们“心有灵犀”的概率为.

知识点

古典概型的概率

题型：简答题

简答题 · 12 分

为拉动经济增长，某市决定新建一批重点工程，分别为基础设施工程、民生工程和产业建设工程三类，这三类工程所含项目的个数分别占总数的、、.现有3名工人独立地从中任选一个项目参与建设.求：

（1）他们选择的项目所属类别互不相同的概率；

（2）至少有1人选择的项目属于民生工程的概率.

正确答案

（1）（2）

解析

解析：记第名工人选择的项目属于基础设施工程、民生工程和产业建设工程分别为事件i=1，2，3.由题意知相互独立，相互独立，

相互独立，（i，j，k=1，2，3，且i，j，k互不相同）相互独立，

且

（1）他们选择的项目所属类别互不相同的概率

（2）至少有1人选择的项目属于民生工程的概率

知识点

古典概型的概率相互独立事件的概率乘法公式

题型：简答题

简答题 · 10 分

某商场在节日期间搞有奖促销活动，凡购买一定数额的商品，就可以摇奖一次，摇奖办法是在摇奖机中装有大小、质地完全一样且分别标有数字1～9的九个小球，一次摇奖将摇出三个小球，规定：摇出三个小球号码是“三连号”（如1、2、3）的获一等奖，奖1000元购物券；若三个小球号码“均是奇数或均是偶数”的获二等奖，奖500元购物券；若三个小球号码中有一个是“8”的获三等奖，奖200元购物券；其他情形则获参与奖，奖50元购物券，所有获奖等第均以最高奖项兑现，且不重复兑奖，记X表示一次摇奖获得的购物券金额。

（1）求摇奖一次获得一等奖的概率；

（2）求X的概率分布列和数学期望。

正确答案

见解析。

解析

（1）记“摇奖一次获得一等奖”为事件A，

连号的可能情况有：123，234，345，456，567，678，789共7种情况。

∴P（A）===。

故摇奖一次获得一等奖的概率为。

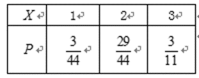
（2）由题设知X的可能取值分别为1000，500，200，50。

P（X=1000）=，P（X=500）==，

P（X=200）==，

P（X=50）===，

∴X的分布列如下：

EX==。

知识点

古典概型的概率离散型随机变量及其分布列、均值与方差

继续学习学习下一知识点

下一知识点 : 与长度、角度有关的几何概型

百度题库 > 高考 > 理科数学 > 古典概型的概率

扫码查看完整答案与解析