- 古典概型的概率
- 共151题
8.形如45132这样的数称为“波浪数”,即十位数字,千位数字均比它们各自相邻的数字大,则由1、2、3、4、5可构成的数字不重复的五位“波浪数”的概率为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.若盒中装有同一型号的灯泡共12只,其中有9只合格品,3只次品。
(1)某工人师傅有放回地连续从该盒中取灯泡3次,每次取一只灯泡,求2次取到次品的概率;
(2)某工人师傅用该盒中的灯泡去更换会议室的一只已坏灯泡,每次从中取一灯泡,若是正品则用它更换已坏灯泡,若是次品则将其报废(不再放回原盒中),求成功更换会议室的已坏灯泡前取出的次品灯泡只数X的分布列和数学期望。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.集合
正确答案
0.6
解析
解析已在路上飞奔,马上就到!
知识点
18.某中学的高二(1)班男同学有


(Ⅰ)求某同学被抽到的概率及课外兴趣小组中男、女同学的人数;
(Ⅱ)经过一个月的学习、讨论,这个兴趣小组决定选出两名同学做某项实验,方法是先从小组里选出
(Ⅲ)试验结束后,第一次做试验的同学得到的试验数据为

正确答案
解:(Ⅰ)
设有


(Ⅱ)把






(Ⅲ)

解析
解析已在路上飞奔,马上就到!
知识点
8.如下图是某位篮球运动员8场比赛得分的茎叶图,其中一个数据染上污渍用
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19. 有甲乙两个班级进行数学考试,按照大于等于85分为优秀,85分以下为非优秀统计成绩后,得到如下的列联表.
已知在全部105人中抽到随机抽取1人为优秀的概率为
(1)请完成上面的列联表;
(2)根据列联表的数据,若按
(3)若按下面的方法从甲班优秀的学生抽取一人:把甲班优秀的10名学生从2到11进行编号,先后两次抛掷一枚均匀的骰子,出现的点数之和为被抽取人的序号.试求抽到6或10号的概率.
参考公式:
参考数据:
正确答案
解:(1)
(2)根据列联表中的数据,得到 
因此有95%的把握认为“成绩与班级有关系”.
(3)设“抽到6或10号”为事件A,先后两次抛掷一枚均匀的骰子,出现的点数为(x,y).
所有的基本事件有(1,1)、(1,2)、(1,3)、……、(6,6),共36个.
事件A包含的基本事件有:
(1,5)、(2,4)、(3,3)、(4,2)、
(5,1)(4,6)、(5,5)、(6、4),共8个

解析
解析已在路上飞奔,马上就到!
知识点
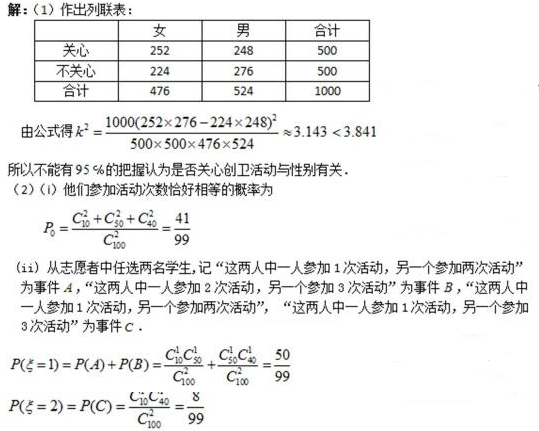
16.(某中学号召本校学生在本学期参加市创办卫生城的相关活动,学校团委对该校学生是否关心创卫活动用简单抽样方法调查了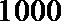
(1)完成列联表,并判断能否有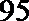
(参考数据与公式: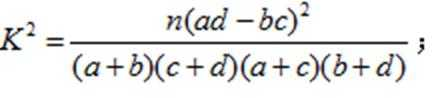
(2)已知校团委有青年志愿者100名,他们已参加活动的情况记录如下:
(i)从志愿者中任选两名学生,求他们参加活动次数恰好相等的概率;
(ii)从志愿者中任选两名学生,用
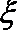

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9. 将一颗骰子掷两次,观察出现的点数并设第一次出现的点数为





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.某种家用电器每台的销售利润与该电器的无故障时间T(单位:年)有关,若T







(Ⅰ)求
(Ⅱ)记

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.集合
所取两数m>n的概率是( ) 。
正确答案
0.6
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析