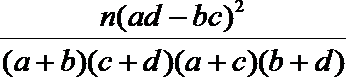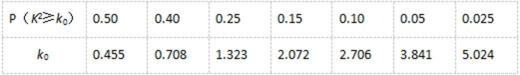- 古典概型的概率
- 共151题
7.将一颗骰子抛掷两次,所得向上点数分别为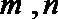
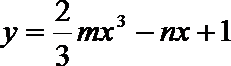

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.某高中为了推进新课程改革,满足不同层次学生的需求,决定从高一年级开始,在每周的周一、周三、周五的课外活动期间同时开设数学、物理、化学、生物和信息技术辅导讲座,每位有兴趣的同学可以在期间的任何一天参加任何一门科目的辅导讲座,也可以放弃任何一门科目的辅导讲座。(规定:各科达到预先设定的人数时称为满座,否则称为不满座)统计数据表明,各学科讲座各天的满座的概率如下表:
根据上表:
(1)求数学辅导讲座在周一、周三、周五都不满座的概率;
(2)设周三各辅导讲座满座的科目数为

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.如图所示的茎叶图表示甲、乙两人在5次综合测评中的成绩,其中一个数字被污损,则甲的平均成绩超过乙的平均成绩的概率为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.投掷两颗骰子,其向上的点数分别为


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.用数字2,3,5,6,7组成没有重复数字的五位数,使得每个五位数中的相邻的两个数都互质,则得到这样的五位数的概率为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.设6张卡片上分别写有函数





(1)现从盒子中任取两张卡片,将卡片上的函数相加得一个新函数,求所得函数是奇函数的概率;
(2)现从盒子中进行逐一抽取卡片,且每次取出后均不放回,若取到一张记有偶函数的卡片,则停止抽取,否则继续进行,求抽取次数
正确答案
解:(1)记事件A为“任取两张卡片,将卡片上的函数相加得到的函数是奇函数”,则
(2)



故ξ的分布列为



解析
解析已在路上飞奔,马上就到!
知识点
8.袋中有大小相同的5个白球和3个黑球,从中任意摸出4个,求摸出2个或3个白球的概率_______________.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
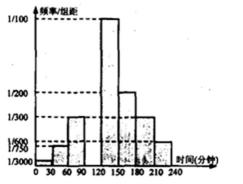
20.某校高一年级共有学生1000名,其中走读生750名,住宿生250名,现从该年级采用分层抽样的方法从该年级抽取n名学生进行问卷调查。根据问卷取得了这n名同学每天晚上有效学习时间(单位:分钟)的数据,按照以下区间分为八组:[0,30),[30,60),[60,90),[90,120),[120,l50),[150,180),[180,210),[210,240),得到频率分布直方图如下图。已知抽取的学生中每天晚上有效学习时间少于60分钟的人数为5人。
(1)求n的值并求有效学习时间在[90,120)内的频率;
(2)如果把“学生晚上有效时间达到两小时”作为是
否充分利用时间的标准,对抽取的n名学生,请
补完整下列2×2列联表并判断是否有95%的把握
认为学生利用时间是否充分与走读、住宿有关?
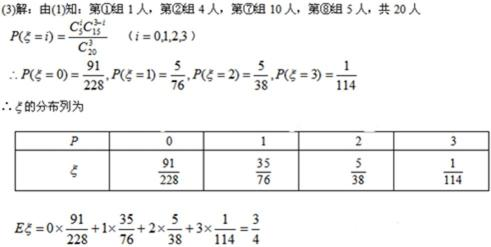
(3)若在第①组、第②组、第⑦组、第⑧组中共抽出3
人调查影响有效利用时间的原因,记抽到“有效学
习时间少于60分钟”的学生人数为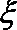
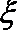
参考公式:K2=
参考列表:
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.在某地奥运火炬传递活动中,有编号为
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.设计某项工程,需要等可能地从4个向量a=(2,3)、b=(1,5)、c=(4,3)、d=(8,1)中任选两个来计算数量积,若所得数量积为随机变量ξ.
(1)求随机变量ξ≤19的概率;
(2)求随机变量ξ的分布列和期望E(ξ).
正确答案
(1)
a·b=2×1+3×5=17,
a·c=2×4+3×3=17,
a·d=2×8+3×1=19,
b·c=1×4+5×3=19
b·d=1×8+5×1=13,
c·d=4×8+3×1=35
P(ξ≤19)=P(ξ=19)+P(ξ=17)+P(ξ=13)=
∴数量积ξ≤19的概率为
(2)数量积ξ可能取值为13,17,19,35,
P(ξ=13)=

P(ξ=19)=
数量积ξ的分布列为
数量积ξ的期望E(ξ)=
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析