- 利用导数求函数的最值
- 共345题
1
题型:填空题
|
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
1
题型:简答题
|
某企业拟建造如图所示的容器(不计厚度,长度单位:米),其中容器的中间为圆柱形,左右两端均为半球形,按照设计要求容器的体积为



(1)写出

(2)求该容器的建造费用最小时的
正确答案
见解析。
解析
(1)因为容器的体积为








(2)因为







知识点
函数解析式的求解及常用方法利用导数求函数的最值
1
题型:简答题
|
设
(1)如果



(2)如果





正确答案
(1) 
解析
(1)已知
又

则

则
(2)要使
又递减区间长度是正整数,所以
b-a为区间长度。又
又b-a为正整数,且m+n<10,所以m=2,n=3或,
知识点
函数解析式的求解及常用方法利用导数研究函数的单调性利用导数求函数的最值
1
题型:
单选题
|
曲线
正确答案
A
解析
知识点
利用导数求函数的最值
1
题型:简答题
|
设函数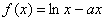
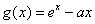
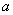
(1)若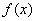
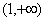
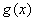

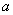
(2)若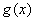

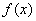
正确答案
见解析
解析
(1)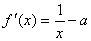
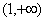
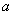
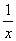
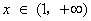
故: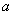
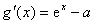
若1≤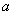
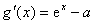
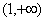
此时,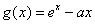

若
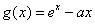
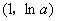
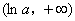
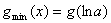
故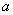

(2)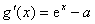

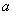
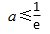
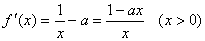
知识点
利用导数研究函数的单调性利用导数求函数的最值
下一知识点 : 利用导数证明不等式
扫码查看完整答案与解析













