- 利用导数求函数的最值
- 共345题
已知f(x)=xlnx,
(1)当a=2时,求函数y=g(x)在[0,3]上的值域;
(2)求函数f(x)在[t,t+2](t>0)上的最小值;
(3)证明:对一切x∈(0,+∞),都有
正确答案
见解析。
解析
(1)
当x=1时,gmin(x)=g(1)=
故g(x)值域为
(2) f'(x)=lnx+l,当

①
②

③

所以
(3)g'(x)+1=x,所以问题等价于证明


设



知识点
已知函数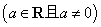
(1)若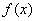
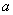
(2)求函数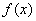
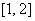
正确答案
见解析。
解析
(1)因为函数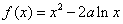
所以函数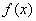
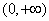
且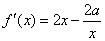
若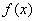
则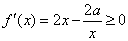
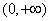
即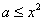
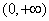
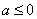
由已知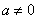
所以实数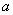
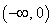
(2)①若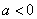
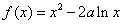
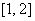
所以函数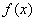
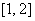
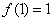
②若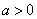
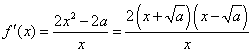
所以函数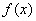
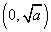
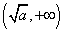
(ⅰ)若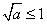
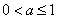
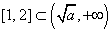
函数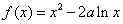
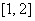
所以函数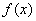
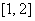
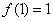
(ⅱ)若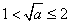
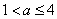
函数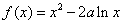
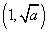
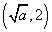
所以函数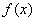
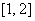
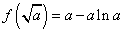
(ⅲ)若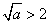
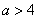
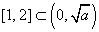
函数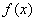
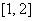
所以函数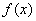
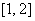
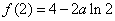
综上所述,当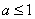
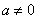
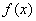
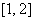
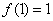
当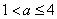
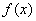
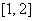
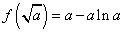
当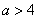
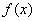
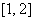
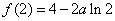
知识点
已知函数
(1)若

(2)若

正确答案
见解析。
解析
(1)若


∵



∴
(2)要使


显然当


∴
当


当



①当



∴

②当



∴

③当





∴
∵


由①②③可得
知识点
21。某旅游景点预计2013年1月份起前x个月的旅游人数的和p(x)(单位:万人)与x的关系近似地满足
(1)写出2013年第x月的旅游人数
(2)试问2013年第几月旅游消费总额最大,最大月旅游消费总额为多少元?
正确答案
见解析。
解析
(1)当

当


验证

(2)第
即
当



解得








当




综上,2013年第5月份的旅游消费总额最大,最大消费总额为3125万元. …12分
知识点
已知函数
(1)若

(2)若对任意


正确答案
(1)
(2)
解析
(1)当


令
列表:
∴当


(2)
① 若

所以,


因为

② 若
所以当
③若

所以,


令
综上,

知识点
扫码查看完整答案与解析