- 一元高次不等式的解法
- 共24题
8.已知函数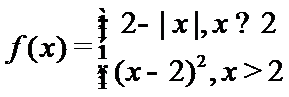
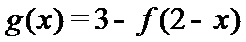
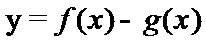
正确答案
解析
当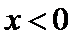
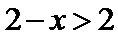
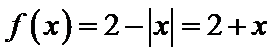
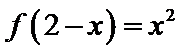
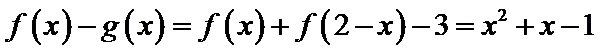
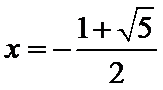
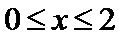
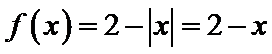
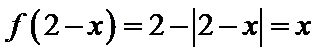
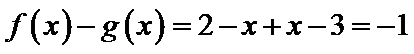
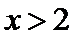
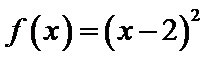
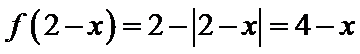
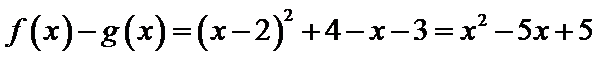
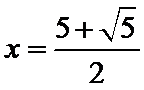
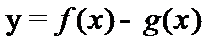
考查方向
解题思路
本题解法采用了直接解方程求零点的方法,这种方法对运算能力要求较高.含有绝对值的分段函数问题,一直是天津高考数学试卷中的热点,这类问题大多要用到数形结合思想与分类讨论思想,注意在分类时要做到:互斥、无漏、最简.
易错点
正确进行分类讨论
知识点
8.某辆汽车每次加油都把油箱加满,下表记录了该车相邻两次加油时的情况.
加油时间
加油量(升)
加油时的累计里程(千米)






注:“累计里程“指汽车从出厂开始累计行驶的路程
在这段时间内,该车每
正确答案
解析
因为第一次邮箱加满,所以第二次的加油量即为该段时间内的耗油量,故耗油量


考查方向
解题思路
由表格信息,得到该车加了48升的汽油,跑了600千米,由此得到该车每100千米平均耗油量.
易错点
实际问题的理解运用
知识点
9.若


正确答案
3
解析
等式组表示的平面区域如图



平移直线



考查方向
解题思路
利用线性规划求最值,一般用图解法求解,其步骤是:
(1)在平面直角坐标系内作出可行域;
(2)考虑目标函数的几何意义,将目标函数进行变形;
(3)确定最优解:在可行域内平行移动目标函数变形后的直线,从而确定最优解;
(4)求最值:将最优解代入目标函数即可求出最大值或最小值.
易错点
可行域的正确作图
知识点
13.若



正确答案

解析
做可行域

考查方向
解题思路
做可行域(如图)作然后作目标函数的直线,平移得到最优解。
易错点
容易出现最优解的错误。
知识点
扫码查看完整答案与解析