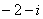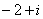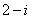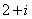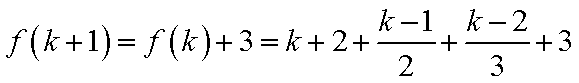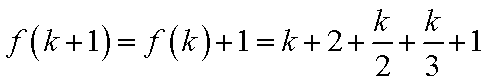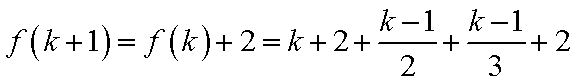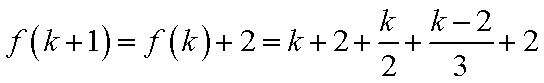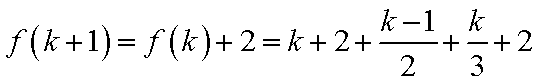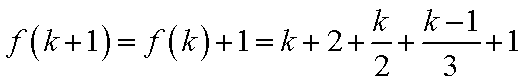- 元素与集合关系的判断
- 共59题
已知集合X={1,2,3},Yn={1,2,3,…,n)(n∈N*),设Sn={(a,b)|a整除b或整除a,a∈X,B∈Yn},令f(n)表示集合Sn所含元素的个数.
36.写出f(6)的值;
37.当n≥6时,写出f(n)的表达式,并用数学归纳法证明.
正确答案
13
解析
(1)f(6)=6+2+

考查方向
解题思路
(1)f(6)=6+2+

易错点
本题在计算时易错.
正确答案
(2)当n≥6时,f(n)=
下面用数学归纳法证明:
①n=6时,f(6)=6+2+

②假设n=k(k≥6)时,结论成立,那么n=k+1时,Sk+1在Sk的基础上新增加的元素在(1,k+1),(2,k+1),(3,k+1)中产生,分以下情形讨论:
1)若k+1=6t,则k=6(t﹣1)+5,此时有f(k+1)=f(k)+3=(k+1)+2+

2)若k+1=6t+1,则k=6t+1,此时有f(k+1)=f(k)+1=k+2+



3)若k+1=6t+2,则k=6t+1,此时有f(k+1)=f(k)+2=k+2+



4)若k+1=6t+3,则k=6t+2,此时有f(k+1)=f(k)+2=k+2+



5)若k+1=6t+4,则k=6t+3,此时有f(k+1)=f(k)+2=k+2+



6)若k+1=6t+5,则k=6t+4,此时有f(k+1)=f(k)+2=k+2+



综上所述,结论对满足n≥6的自然数n均成立.
解析
见答案
考查方向
解题思路
(2)根据数学归纳法的证明步骤,分类讨论,即可证明结论.
易错点
本题考查数学归纳法,在归纳的过程中易错.
若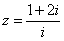
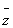
正确答案
解析
知识点
已知集合A={x|x2﹣x﹣6<0},集合B={x|x﹣1>0},则(∁RA)∩B=( )
正确答案
知识点
23.已知集合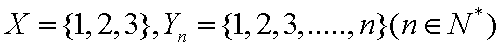

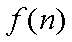
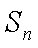
(1)写出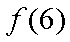
(2)当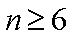
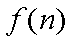
正确答案
(1)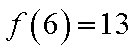
(2)当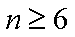
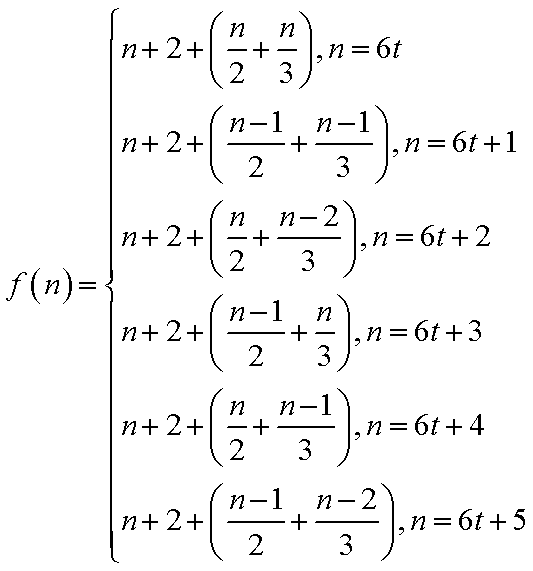
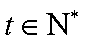
下面用数学归纳法证明:
①当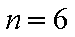
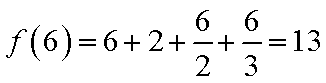
②假设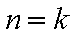
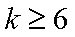
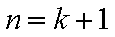
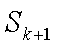
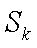
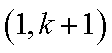
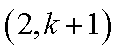
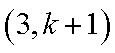
1)若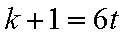
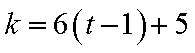
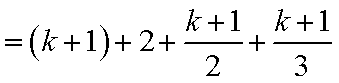
2)若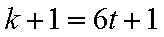
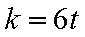
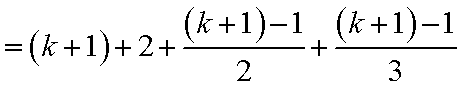
3)若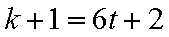
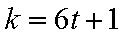
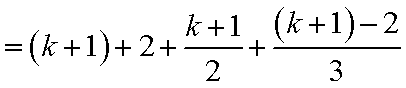
4)若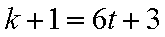
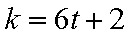
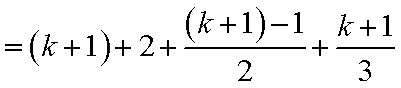
5)若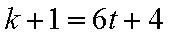
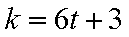
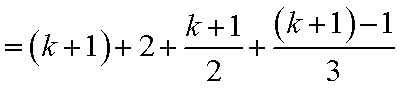
6)若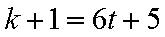
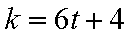
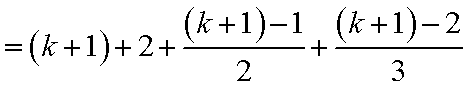
综上所述,结论对满足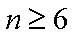
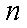
解析
解析已在路上飞奔,马上就到!
知识点
执行如图所示的程序框图,输出的
正确答案
解析
略
知识点
扫码查看完整答案与解析