- 立体几何中的向量方法
- 共7934题
如图,A、D分别是矩形A1BCD1上的点,AB=2AA1=2AD=2,DC=2DD1,把四边形A1ADD1沿AD折叠成直二面角,连接A1B,D1C得几何体ABA1-DCD1.
(1)当点E在棱AB上移动,证明:D1E⊥A1D;
(2)在棱AB上是否存在点E,使二面角D1-EC-D的平面角为
正确答案
解:(1)以D为坐标原点,边DA,DC,DD1所在直线分别为x轴,y轴,z轴建立空间直角坐标系,如图所示:

D(0,0,0),D1(0,0,1),A1(1,0,1),C(0,2,0),设E(1,y0,0),0≤y0≤2;
∴


∴D1E⊥A1D;
(2)假设存在E(1,y0,0)使二面角D1-EC-D的平面角为
DD1⊥平面DCE;
∴
设平面D1CE的一条法向量为

∴
∴
∴平面D1CE的一条法向量为
∴


∴
∴整理得
解得
∴
∴
∴在棱AB上存在点E,使二面角D1-EC-D的平面角为

解析
解:(1)以D为坐标原点,边DA,DC,DD1所在直线分别为x轴,y轴,z轴建立空间直角坐标系,如图所示:

D(0,0,0),D1(0,0,1),A1(1,0,1),C(0,2,0),设E(1,y0,0),0≤y0≤2;
∴


∴D1E⊥A1D;
(2)假设存在E(1,y0,0)使二面角D1-EC-D的平面角为
DD1⊥平面DCE;
∴
设平面D1CE的一条法向量为

∴
∴
∴平面D1CE的一条法向量为
∴


∴
∴整理得
解得
∴
∴
∴在棱AB上存在点E,使二面角D1-EC-D的平面角为




(1)求证:A1B1⊥平面AA1C;
(2)求证:AB1∥平面A1C1C;
(3)求二面角C1-A1C-A的余弦值.
正确答案
(1)证明:∵
∵AA1⊥平面ABC,∴AA1⊥AB
∵AA1∩AC=A
∴AB⊥平面AA1C
∵AA1平行且BB1,
∴四边形ABB1A1为平行四边形
∴A1B1∥AB
∴A1B1⊥平面AA1C;
(2)证明:取BC的中点D,连接AD,DC1,则CD平行且等于B1C1,BD平行且等于B1C1,
∴四边形B1DCC1和BDC1B1为平行四边形
∴B1D平行且等于CC1,∴C1D平行且等于B1B
由(1)B1B平行且等于AA1,∴C1D平行且等于A1A
∴四边形AA1C1D为平行四边形
∴AD∥A1C1∵B1D∩AD=D,B1D,AD⊂平面AB1D
∴平面AB1D∥平面A1C1C
∵AB1⊂平面AB1D
∴AB1∥平面A1C1C;
(3)解:由(1)知,AA1,AB,AC两两垂直,建立如图所示的直角坐标系,设BC=2,则A1(0,0,

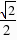


∴



设平面A1C1C的法向量为


∵平面A1AC的法向量为
∴cos

∵二面角C1-A1C-A的为钝二面角,∴二面角C1-A1C-A的余弦值为-
解析
(1)证明:∵
∵AA1⊥平面ABC,∴AA1⊥AB
∵AA1∩AC=A
∴AB⊥平面AA1C
∵AA1平行且BB1,
∴四边形ABB1A1为平行四边形
∴A1B1∥AB
∴A1B1⊥平面AA1C;
(2)证明:取BC的中点D,连接AD,DC1,则CD平行且等于B1C1,BD平行且等于B1C1,
∴四边形B1DCC1和BDC1B1为平行四边形
∴B1D平行且等于CC1,∴C1D平行且等于B1B
由(1)B1B平行且等于AA1,∴C1D平行且等于A1A
∴四边形AA1C1D为平行四边形
∴AD∥A1C1∵B1D∩AD=D,B1D,AD⊂平面AB1D
∴平面AB1D∥平面A1C1C
∵AB1⊂平面AB1D
∴AB1∥平面A1C1C;
(3)解:由(1)知,AA1,AB,AC两两垂直,建立如图所示的直角坐标系,设BC=2,则A1(0,0,

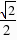


∴



设平面A1C1C的法向量为


∵平面A1AC的法向量为
∴cos

∵二面角C1-A1C-A的为钝二面角,∴二面角C1-A1C-A的余弦值为-


(I)求证:EF∥平面AA1B1B;
(II)求二面角C-A1C1-D的大小.
正确答案

∴OF∥CC1,CC1∥BB1,∴OF∥BB1,又OE∥AB,
∴平面OEF∥平面AA1B1B,又EF⊂平面OEF,
∴EF∥平面AA1B1B.(4分)
(Ⅱ)解:∵AD=1,AA1=2,
∵侧面AD1⊥平面ABCD,∴A1D⊥平面ABCD,可知DA1、DA、DC两两垂直.(6分)
分别以DA1、DA、DC为x、y、z轴建立空间直角坐标系D-xyz,则
D(0,0,0),A(1,0,0),

∴




由


设平面ACC1A1的法向量为
由

则
∴二面角C-A1C1-D的大小为
解析

∴OF∥CC1,CC1∥BB1,∴OF∥BB1,又OE∥AB,
∴平面OEF∥平面AA1B1B,又EF⊂平面OEF,
∴EF∥平面AA1B1B.(4分)
(Ⅱ)解:∵AD=1,AA1=2,
∵侧面AD1⊥平面ABCD,∴A1D⊥平面ABCD,可知DA1、DA、DC两两垂直.(6分)
分别以DA1、DA、DC为x、y、z轴建立空间直角坐标系D-xyz,则
D(0,0,0),A(1,0,0),

∴




由


设平面ACC1A1的法向量为
由

则
∴二面角C-A1C1-D的大小为


(1)求证:AC⊥BF;
(2)求二面角F-BD-A的余弦值.
正确答案
(1)证明:∵AB=1,BC=AD=2,∠ADC=60°,
∴AC2=1+4-2×1×2×cos60°=3
∴AC=
又∵AB=1,BC=2
∴∠BAC=∠ACD=90°,
∴AC⊥AB
又AF⊥AC,AB∩AF=A
∴AC⊥平面ABF,
又∵BF⊂平面ABF,
∴AC⊥BF;
(2)解:建立如图所示的坐标系,则C(0,0,0),D(1,0,0),A(0,



平面ABD的一个法向量
设平面FBD的法向量为
∵



由
令z=1,得

∴
故所求二面角F-BD-A的余弦值为
解析
(1)证明:∵AB=1,BC=AD=2,∠ADC=60°,
∴AC2=1+4-2×1×2×cos60°=3
∴AC=
又∵AB=1,BC=2
∴∠BAC=∠ACD=90°,
∴AC⊥AB
又AF⊥AC,AB∩AF=A
∴AC⊥平面ABF,
又∵BF⊂平面ABF,
∴AC⊥BF;
(2)解:建立如图所示的坐标系,则C(0,0,0),D(1,0,0),A(0,



平面ABD的一个法向量
设平面FBD的法向量为
∵



由
令z=1,得

∴
故所求二面角F-BD-A的余弦值为

(1)证明:A1C⊥平面BED;
(2)求二面角A1-DE-B的余弦值.
正确答案

则A1(2,0,4),B(2,2,0),C(0,2,0),D(0,0,0),E(0,2,1)



∵

∴

∴A1C⊥平面BED
(2)∵

设平面A1DE的法向量为
由

得-2x+2y-3z=0,-2x-4z=0,
取
同理得平面BDE的法向量为
∴cos<



所以二面角A1-DE-B的余弦值为
解析

则A1(2,0,4),B(2,2,0),C(0,2,0),D(0,0,0),E(0,2,1)



∵

∴

∴A1C⊥平面BED
(2)∵

设平面A1DE的法向量为
由

得-2x+2y-3z=0,-2x-4z=0,
取
同理得平面BDE的法向量为
∴cos<



所以二面角A1-DE-B的余弦值为

(1)求CD的长;
(2)求证:AF⊥BD;
(3)求平面ADF与平面ABC所形成的较小的二面角的度数.
正确答案

又AE和CD都垂直于平面ABC,∴AE∥CD,
∴FG∥CD,∴F、G、C、D四点共面.
又平面FGCD∩平面ABC=CG,DF∥平面ABC,
∴DF∥CG,∴四边形FGCD是平行四边形,∴
(2)证明:直角三角形ABE中,AE=AB,F是BE的中点,∴AF⊥BE,
又△ABC中,AC=BC,G是AB中点,∴CG⊥AB,又AE垂直于平面ABC,∴AE⊥CG,
又AE∩AB=A,∴CG⊥面ABE.∵DF∥CG,∴DF⊥面ABE,∴AF⊥DF
又∵BE∩DF=F,∴AF⊥面BED,∴AF⊥BD.
(3)解:设面ADF∩面ABC=L,∵DF∥平面ABC,∴DF∥L,
又DF⊥面ABE,∴L⊥面ABE,∴L⊥AF,L⊥AB,
∴∠FAB即为所求二面角的平面角.直角三角形ABE中,易得∠FAB=45°
∴平面ADF与平面ABC所形成的较小的二面角为45°.
解析

又AE和CD都垂直于平面ABC,∴AE∥CD,
∴FG∥CD,∴F、G、C、D四点共面.
又平面FGCD∩平面ABC=CG,DF∥平面ABC,
∴DF∥CG,∴四边形FGCD是平行四边形,∴
(2)证明:直角三角形ABE中,AE=AB,F是BE的中点,∴AF⊥BE,
又△ABC中,AC=BC,G是AB中点,∴CG⊥AB,又AE垂直于平面ABC,∴AE⊥CG,
又AE∩AB=A,∴CG⊥面ABE.∵DF∥CG,∴DF⊥面ABE,∴AF⊥DF
又∵BE∩DF=F,∴AF⊥面BED,∴AF⊥BD.
(3)解:设面ADF∩面ABC=L,∵DF∥平面ABC,∴DF∥L,
又DF⊥面ABE,∴L⊥面ABE,∴L⊥AF,L⊥AB,
∴∠FAB即为所求二面角的平面角.直角三角形ABE中,易得∠FAB=45°
∴平面ADF与平面ABC所形成的较小的二面角为45°.

(1)求证:AB1⊥平面A1BD;
(2)求二面角A-A1D-B的余弦值.
正确答案
(1)
∵在正三棱柱ABC-A1B1C1中,平面ABC⊥平面BCC1B1,∴AO⊥平面BCC1B1,
取B1C1中点为O1,以O为原点,


则
∴


∵

∴

∴AB1⊥面A1BD.
(2)设平面A1AD的法向量为


∴


令z=1,得
∴

由图可以看出:二面角A-A1D-B是锐角.
∴二面角A-A1D-B的余弦值为
解析
(1)
∵在正三棱柱ABC-A1B1C1中,平面ABC⊥平面BCC1B1,∴AO⊥平面BCC1B1,
取B1C1中点为O1,以O为原点,


则
∴


∵

∴

∴AB1⊥面A1BD.
(2)设平面A1AD的法向量为


∴


令z=1,得
∴

由图可以看出:二面角A-A1D-B是锐角.
∴二面角A-A1D-B的余弦值为
如图,已知菱形ABCD的边长为6,∠BAD=60°,AC∩BD=O.将菱形ABCD沿对角线AC折起,使BD=3
(Ⅰ)若点M是棱BC的中点,求证:OM∥平面ABD;
(Ⅱ)求二面角A-BD-O的余弦值;
(Ⅲ)设点N是线段BD上一个动点,试确定N点的位置,使得CN=4
正确答案
解:
所以O是AC的中点.又点M是棱BC的中点,
所以OM是△ABC的中位线,OM∥AB.…(1分)
因为OM⊄平面ABD,AB⊂平面ABD,
所以OM∥平面ABD.…(3分)
(Ⅱ)由题意,OB=OD=3,
因为
所以∠BOD=90°,OB⊥OD.…(4分)
又因为菱形ABCD,所以OB⊥AC,OD⊥AC.
.
所以
设平面ABD的法向量为n=(x,y,z),
则有
令x=1,则

因为AC⊥OB,AC⊥OD,所以AC⊥平面BOD.
平面BOD的法向量与AC平行,
所以平面BOD的法向量为n0=(1,0,0).…(8分)
∴
因为二面角A-BD-O是锐角,
所以二面角A-BD-O的余弦值为
(Ⅲ)因为N是线段BD上一个动点,设N(x1,y1,z1),
则(x1,y1,z1-3)=λ(0,3,-3),
所以x1=0,y1=3λ,z1=3-3λ,…(10分)
则N(0,3λ,3-3λ),
由

解得

所以N点的坐标为(0,2,1)或(0,1,2).…(13分)
(也可以答是线段BD的三等分点,

解析
解:
所以O是AC的中点.又点M是棱BC的中点,
所以OM是△ABC的中位线,OM∥AB.…(1分)
因为OM⊄平面ABD,AB⊂平面ABD,
所以OM∥平面ABD.…(3分)
(Ⅱ)由题意,OB=OD=3,
因为
所以∠BOD=90°,OB⊥OD.…(4分)
又因为菱形ABCD,所以OB⊥AC,OD⊥AC.
.
所以
设平面ABD的法向量为n=(x,y,z),
则有
令x=1,则

因为AC⊥OB,AC⊥OD,所以AC⊥平面BOD.
平面BOD的法向量与AC平行,
所以平面BOD的法向量为n0=(1,0,0).…(8分)
∴
因为二面角A-BD-O是锐角,
所以二面角A-BD-O的余弦值为
(Ⅲ)因为N是线段BD上一个动点,设N(x1,y1,z1),
则(x1,y1,z1-3)=λ(0,3,-3),
所以x1=0,y1=3λ,z1=3-3λ,…(10分)
则N(0,3λ,3-3λ),
由

解得

所以N点的坐标为(0,2,1)或(0,1,2).…(13分)
(也可以答是线段BD的三等分点,


(Ⅰ)证明:AC=AB1;
(Ⅱ)若AC⊥AB1,∠CBB1=60°,AB=BC,求二面角A-A1B1-C1的余弦值.
正确答案
解:(1)连结BC1,交B1C于点O,连结AO,
∵侧面BB1C1C为菱形,
∴BC1⊥B1C,且O为BC1和B1C的中点,
又∵AB⊥B1C,∴B1C⊥平面ABO,
∵AO⊂平面ABO,∴B1C⊥AO,
又B10=CO,∴AC=AB1,
(2)∵AC⊥AB1,且O为B1C的中点,∴AO=CO,
又∵AB=BC,∴△BOA≌△BOC,∴OA⊥OB,
∴OA,OB,OB1两两垂直,
以O为坐标原点,



∵∠CBB1=60°,∴△CBB1为正三角形,又AB=BC,
∴A(0,0,


∴








设向量
则



同理可得平面A1B1C1的一个法向量


∴cos<



∴二面角A-A1B1-C1的余弦值为
解析
解:(1)连结BC1,交B1C于点O,连结AO,
∵侧面BB1C1C为菱形,
∴BC1⊥B1C,且O为BC1和B1C的中点,
又∵AB⊥B1C,∴B1C⊥平面ABO,
∵AO⊂平面ABO,∴B1C⊥AO,
又B10=CO,∴AC=AB1,
(2)∵AC⊥AB1,且O为B1C的中点,∴AO=CO,
又∵AB=BC,∴△BOA≌△BOC,∴OA⊥OB,
∴OA,OB,OB1两两垂直,
以O为坐标原点,



∵∠CBB1=60°,∴△CBB1为正三角形,又AB=BC,
∴A(0,0,


∴








设向量
则



同理可得平面A1B1C1的一个法向量


∴cos<



∴二面角A-A1B1-C1的余弦值为


(1)求四棱锥B1-AECD的体积;
(2)证明:B1E∥面ACF;
(3)求面ADB1与面ECB1所成锐二面角的余弦值.
正确答案


所以△ABE为等边三角形,所以
又因为面B1AE⊥面AECD,所以B1M⊥面AECD,…(2分)
所以
(Ⅱ)证明:连接ED交AC于O,连接OF,因为AECD为菱形,OE=OD,
又F为B1D的中点,所以FO∥B1E,
因为FO⊂面ACF
所以B1E∥面ACF…(7分)
(Ⅲ)解:连接MD,分别以ME,MD,MB1为x,y,z轴,建立空间直角坐标系.
则
设面ECB1的法向量

令x‘=1,则
设面ADB1的法向量为

令x=1,则
则
所以二面角的余弦值为
解析


所以△ABE为等边三角形,所以
又因为面B1AE⊥面AECD,所以B1M⊥面AECD,…(2分)
所以
(Ⅱ)证明:连接ED交AC于O,连接OF,因为AECD为菱形,OE=OD,
又F为B1D的中点,所以FO∥B1E,
因为FO⊂面ACF
所以B1E∥面ACF…(7分)
(Ⅲ)解:连接MD,分别以ME,MD,MB1为x,y,z轴,建立空间直角坐标系.
则
设面ECB1的法向量

令x‘=1,则
设面ADB1的法向量为

令x=1,则
则
所以二面角的余弦值为
扫码查看完整答案与解析















