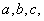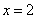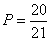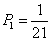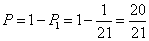- 函数y=Asin(ωx+φ)的应用
- 共30题
已知函数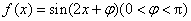
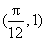
(1)求
(2)在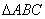
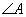
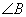
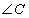
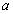
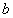
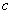
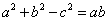
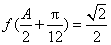
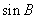
正确答案
见解析。
解析
知识点
函数



正确答案
解析
略
知识点
一艘轮船在匀速行驶过程中每小时的燃料费与它速度的平方成正比,除燃料费外其它费用为每小时



正确答案
40
解析
略
知识点
已知函数
(1)求函数
(2)若



正确答案
见解析。
解析
知识点
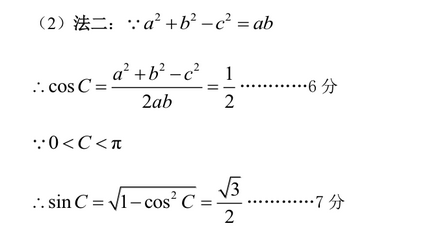
若△ABC的内角A,B,C所对的边a,b,c满足(a+b)2﹣c2=ab,则C等于( )
正确答案
解析
由条件利用余弦定理可得 cosC=﹣

解:∵△ABC的内角A,B,C所对的边a,b,c满足(a+b)2﹣c2=ab,
由余弦定理可得 c2=a2+b2﹣2ab•cosC,
化简可得 cosC=﹣

故选C。
知识点
在

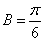
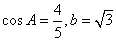
(1)求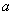
(2)求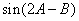
正确答案
见解析。
解析
(1)交警小李对进站休息的驾驶人员的省籍询问采用的是系统抽样方法.
(2)从图中可知,被询问了省籍的驾驶人员广西籍的有: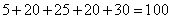
四川籍的有: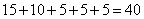
设四川籍的驾驶人员应抽取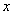
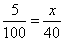
即四川籍的应抽取2名.
(3)(方法1)用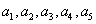
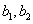

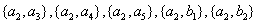
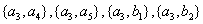
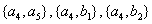

其中至少有1名驾驶人员是广西籍的基本事件的总数为:

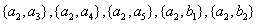
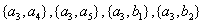
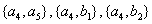
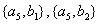
所以,至少有1名驾驶人员是广西籍的概率为
(方法2)所有基本事件的总数同方法1,
其中,2名驾驶人员都是四川籍的基本事件为: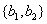
所以,抽取的2名驾驶人员都是四川籍的概率为
所以,至少有1名驾驶人员是广西籍的概率为
知识点
设


正确答案
解析
略
知识点
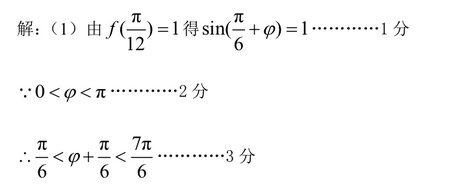
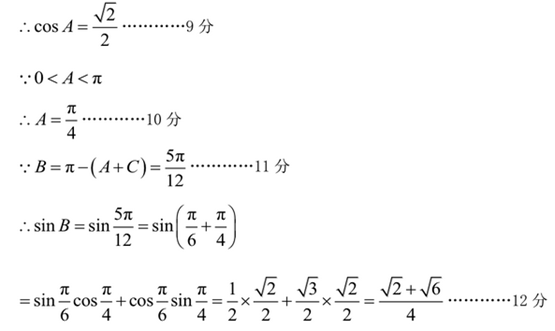
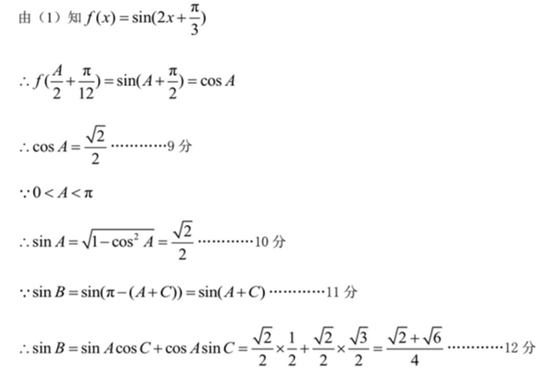
在







(1)求角
(2)若

正确答案
(1)
(2)
解析
(1)解:






(2)解:由正弦定理




知识点
已知函数
(1)求函数
(2)若


正确答案
见解析。
解析
(1)∵

∴函数


(2)∵

∵

又∵

∴原式
知识点
已知函数
(1)求函数
(2)若

正确答案
见解析
解析
(1)∵

由

故函数


(2)由

考察函数

于是
故

知识点
扫码查看完整答案与解析